Системы диагностирования. Алгоритмы диагностирования и методы их построения, страница 7

          Условные алгоритмы также представляются в виде графов. Построение условного алгоритма начинается с выбора первой проверки. В зависимости от исхода первой проверки  множество возможных состояний  делится на два подмножества  и , после чего выбираются проверки (они могут быть разными), разделяющие эти подмножества. Выбор проверок продолжается до тех пор, пока множество  не будет разделено на отдельные подмножества эквивалентных состояний. На рис. 2.12, б приведен условный алгоритм, построенный по табл. 2.2.

          Для одного и того же словаря неисправностей может быть построено значительное количество безусловных и условных алгоритмов диагностирования. Каждый из них будет обладать определенными особенностями. Например, условный алгоритм (рис. 2.12, б) имеет преимущество по сравнению с безусловным алгоритмом (рис. 2.12, а), которое состоит в том, что в первом любая неисправность может быть обнаружена не более чем за три шага алгоритма, в то время как во втором может потребоваться выполнение и четырех шагов алгоритма. Но, с другой стороны, безусловный алгоритм дает возможность обнаружить неисправность уже при выполнении первого шага, а в условном алгоритме такой возможности нет.

          При решении практических задач возникает проблема выбора оптимального алгоритма диагностирования. При этом формулируются либо ограничения на алгоритм, либо критерий оптимальности, в которых отражаются конкретные практические условия применения алгоритма. В качестве ограничения на алгоритм могут выступать: заданное время, в течение которого должна быть обнаружена любая неисправность; максимально допустимое число шагов алгоритма; ограничения, определяющие необходимость обнаружения на первых шагах алгоритма некоторых указанных неисправностей и т.п. В качестве критерия оптимальности может рассматриваться средняя стоимость обнаружения отказавшего элемента, вероятность обнаружения при ограниченной стоимости или стоимость с заданной вероятностью и т.д. В этом случае каждый алгоритм, заданный соответствующим графом, характеризуется определенным значением критерия оптимальности.

          При оптимизации алгоритма, как правило, учитывают три фактора: вероятности отказов элементов модели объекта (или вероятности попадания системы в рассматриваемые состояния); стоимость каждой проверки, под которой понимается некоторое относительное число, отражающее в условных единицах затраты труда, времени, сложность действий,  необходимую аппаратуру и т.п., требующиеся для проведения проверки; величину информации, которую дает каждая проверка. Вероятности отказов элементов задаются при проектировании ОД на этапе выбора элементной базы. Стоимости проверок определяются на основе специального анализа объекта диагноза. При этом выбирается самая сложная проверка и ее стоимость оценивается в 100 условных единиц. Все остальные проверки ранжируются относительно самой сложной проверки и им сопоставляются соответствующие оценочные стоимости. Информация о состоянии объекта, которую можно получить при выполнении той или другой проверки, содержится в таблицах, соответствующих словарям неисправностей.

          Наиболее общим критерием оптимальности является средняя стоимость выполнения алгоритма. Рассмотрим алгоритмы, заданные графами на рис. 2.12. Зададим вероятности состояний: = 0,2  и = 0,1, а также стоимости проверок: = 50,  = 40,  = 30, = 20.

          Средняя стоимость выполнения алгоритма

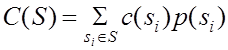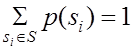,      ,                  (2.14)

где  – множество всех состояний системы;

      – суммарная стоимость всех проверок, выполнение которых необходимо для выделения состояния  в соответствии с данным алгоритмом; сумма вероятностей состояний равна единице, так как алгоритм применяется тогда, когда система находится в одном из состояний .