Системы диагностирования. Алгоритмы диагностирования и методы их построения, страница 8

          В условном алгоритме (рис. 2.12, б) для выделения, например, состояния  необходимо последовательно применить проверки ,  и . Поэтому

.

          В целом для данного алгоритма имеем

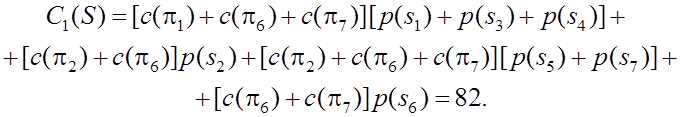
          Различные алгоритмы сравнивают по численному значению . Например, для безусловного алгоритма (см. рис. 2.12, а) = 103, и поэтому он хуже условного алгоритма (см. рис. 2.12, б), так как  . Очевидно, что при других соотношениях между вероятностями  и стоимостями , безусловный алгоритм может оказаться предпочтительнее условного. Для нахождения алгоритма с минимальной стоимостью  используют перебор вариантов или принципы динамического программирования, что связано со сложными вычислительными процедурами. Поэтому на практике часто применяют некоторые решающие правила (упрощенные подходы), которые позволяют находить близкие к оптимальным алгоритмы. Часто возникает такая задача. Имеется система, состоящая из  элементов, один из которых неисправен. Для каждого элемента известны вероятность  возникновения неисправности и стоимость  его проверки  (в большинстве случаев в качестве  выступает время проверки элемента). В этом случае последовательность проверок в алгоритме устанавливается в соответствии с порядком соотношений . При этом если после проведения  проверки неисправный элемент не обнаружен, то, вследствие того что 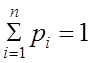, за неисправный принимается последний элемент и его не проверяют.

          При построении алгоритмов диагностирования существенное значение имеет количество информации, содержащееся в проверках. Частично это учитывается и при оптимизации алгоритмов с помощью выражения (2.14). Более полный учет позволяет получить метод, основанный на теории информации.

          Диагностирование есть по сути своей процесс получения информации о состоянии объекта. Перед началом процесса диагностирования объект с точки зрения наблюдателя обладает большой степенью неопределенности состояния. Она будет тем больше, чем больше число возможных состояний и чем меньше разброс их вероятностей. Неопределенность состояния системы  характеризуется ее энтропией  . Если система из  элементов может быть  неисправной  в результате отказа только одного какого-либо -го элемента с условной вероятностью отказа , то

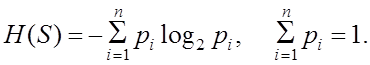                      (2.15)

          Значения  определяются на основе статистических данных о надежности элементов системы.

          Для энтропии характерны следующие свойства:

          1) ;

          2) энтропия системы, имеющей   равновероятных состояний

;

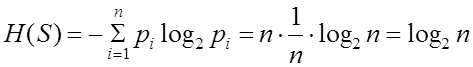          3) энтропия системы максимальна, если ее состояния равновероятны;

          4) если  = 1, то .

          Каждая проверка  содержит некоторое количество информации  относительно состояния системы :

,                            (2.16)

где – средняя условная энтропия состояния системы при выполнении проверки .

          Если при проверке  контролируется  элементов системы, сумма вероятностей отказов которых 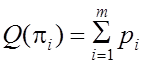, то

.  (2.17)

          При построении алгоритма в качестве первой проверки выбирают ту, которая несет наибольшее количество информации. Из выражения (2.17) следует, что  принимает максимальное значение при 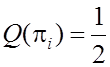.  Поэтому алгоритм следует начинать с проверки, для которой сумма вероятностей отказов проверяемых элементов близка к  . Следующую проверку выбирают исходя из результатов предыдущей. Если при проверке  получен результат  ( или ), из которого следует, что система находится в одном из состояний подмножества , то следующую проверку  выбирают по максимуму количества информации в системе :

.                   (2.18)

          В этом случае значения  пересчитываются с учетом равенства

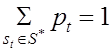.                                            (2.19)

          Построим алгоритм по табл. 2.2. Для каждой проверки  значения , представляющие собой сумму вероятностей отказов тех элементов, которые проверяются данной проверкой, равны:

………              

.…0,3    0,2     0,6     0,5

Так как 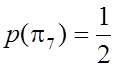, то в качестве первой проверки выбираем проверку  (рис. 2.13).

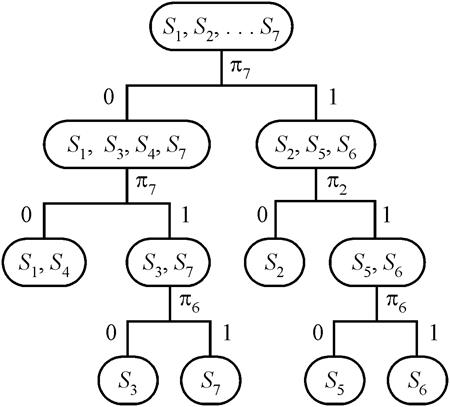
Рис.2.13. Схема алгоритма диагностирования