Системы диагностирования. Алгоритмы диагностирования и методы их построения, страница 3

          В таблице отражены восемь возможных случаев сочетаний независимых событий, отражаемых вероятностями ,  и . Например, в шестой строке таблицы указаны значения = 1, = 0 и = 1. Эта строка соответствует случаю, когда исходный ОД работает правильно (= 1), схема контроля отказала (= 0), а метод контроля обнаружил этот отказ (= 1). Данное событие имеет результатом появление на выходе СК сигнала ошибки (см. рис. 2.3). Поэтому в столбце , который соответствует событию обнаружения ошибок, в шестой строке проставляется единичное значение функции. Такое же значение проставляется в строках 2 и 4, где = 1 и имеют место дефекты в ОД или СК. В столбце  единичное значение функции проставляется только в строках 7 и 8, которые соответствуют случаю, когда и ОД, и СК работают правильно. В столбце  единичное значение функции заносится в строки, где = 0, кроме седьмой строки, в которой = 1  и  = 1.

          Из таблицы следует, что

,

 ,            (2.4)

.

          От булевых функций осуществляется переход к вероятностным выражениям. При этом сначала производится упрощение выражений (2.4) по законам алгебры логики без использования закона повторения. Соответствующие преобразования дают следующие выражения:

,

,                          (2.5)

.

          При переходе к вероятностным выражениям  знак дизъюнкции заменяется знаком сложения, а переменная  заменяется выражением . В результате получаем:

,

,                  (2.6)

.

          Из (2.6) следует, что достоверность ОД с аппаратным контролем

.                 (2.7)

          Если контроль отсутствует (в этом случае = 1 и = 0), то достоверность ОД без контроля

 .                                            (2.8)

          Выигрыш в достоверности при использовании контроля

.           (2.9)

          Однако выигрыш в достоверности сопровождается проигрышем в надежности и увеличением сложности устройства. Введение контроля снижает вероятность безотказной работы ОД с контролем. Действительно, вероятность правильной работы ОД со схемой контроля равна вероятности безотказной работы ОД со схемой контроля, т.е.

.                                     (2.10)

          Тогда проигрыш в безотказности

 .                                      (2.11)

          Усложнение объекта характеризуется коэффициентом

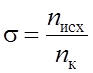,                                                (2.12)

где   и – число элементов соответственно в исходном устройстве и схеме контроля.

          При решении конкретных задач возникает вопрос о допустимом коэффициенте избыточности. Существует стандартный способ построения СК – метод дублирования (см. рис. 2.4).

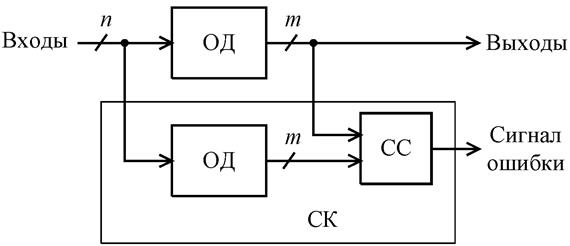
Рис.2.4. Схема дублирования

В этом случае СК включает в себя второй комплект ОД и схему сравнения выходных сигналов обоих комплектов. Для схемы дублирования

,

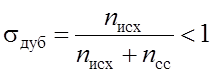где  – число элементов в схеме сравнения.

          На практике стремятся получить системы диагностирования со сложностью . Наилучшими считаются варианты систем с  (контрольное оборудование не превышает 10%), достаточно хорошими – вариант с  (не более 25%). Увеличение выигрыша в достоверности, как правило, требует усложнения контрольного оборудования.

          Из формул (2.9) и (2.11) следует, что чем выше , тем больше выигрыш в достоверности, при этом проигрыш в безотказности остается на прежнем уровне. Поэтому следует применять более совершенные методы контроля. Однако существует определенная взаимосвязь между  и , так как более совершенные методы контроля требуют более сложного контрольного оборудования.

          При организации функционального диагностирования возникает задача контроля исправности СК (проблема «сторожа над сторожем»). Если применяемый метод контроля не позволяет обнаруживать неисправности СК, то достоверность ОД с контролем уменьшается и подсчитывается по формуле

.                    (2.13)

          При синтезе дискретных устройств с контролем задача контроля СК решается за счет придания ДУ свойства самопроверяемости. Под самопроверяемостью понимается способность системы обнаруживать отказы как в основном устройстве, так и в схеме контроля, в процессе нормального функционирования без дополнительной подачи на входы устройства специальных проверочных тестов или других способов его испытания.