Петербургский Государственный Университет Путей Сообщения
Кафедра: «Экономика транспорта»
Отчет по лабораторной работе №2
Использование электронных таблиц для расчета основных функций финансового менеджмента
|
Выполнил студент группы АТ-705 Королев И.Н. |
Проверила Котова Е. А. |
Санкт - Петербург
2011
Среди функций аннуитета наиболее часто применяется функции регулярного платежа - Payment или сокращенно РМТ в случае обслуживания займов, кредитов и в других операциях.
Предположим нами взят кредит на приобретение оборудования, рассчитать размер PMT - ежемесячных платежей по возврату кредита, если известен размер кредита - наш основной капитал - Principal - (Prin), размер ставки банковского процента (i), под который был взят кредит и срок отдачи ссуды (n), который может исчисляться в месяцах или годах. Если срок отдачи кредита задан в месяцах, расчет выполняется по формуле:
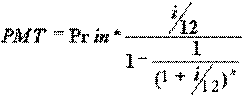
Ставка кредита в этой формуле задается в десятичных дробях. Пример. Пусть Prin=$1000, i=10% - (0.1), n=5 месяцев. PMT=$205 в месяц. Это означает, что при ставке 10% годовых, взятый нами кредит в $1000 мы должны отдавать равными долями по $205 в течение 5 месяцев.
|
PMT |
=PMT(D2/12;D3;D4) |
=PMT(E2;E3*12;E4) |
=PMT |
=PMT |
||
|
Rate |
Ставка |
Ставка |
0,1 |
0,1 |
0,2 |
0,2 |
|
nper |
кпер |
кпер |
6 |
6 |
6 |
1 |
|
pv |
нз |
пс |
10000 |
10000 |
8000 |
8000 |
|
PMT |
ППЛАТ |
ПЛТ |
-1 715,61р. |
-1 001,05р. |
-1 412,18р. |
-1 802,12р. |
Предположим мы желаем накопить определенную сумму в банке, которая в будущем составит определенное значение - FV (Future Value). Задан размер PMT - ежемесячных платежей, которые мы рассчитываем выплачивать и размер ставки банковского процента (i) Найти срок, в течение которого желаемая сумма FV будет накоплена. Расчет TERM выполняется по формуле:
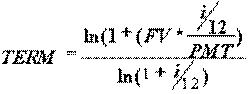
Пример. Пусть FV=$1000, i=10% - (0,1), PMT=$100 в месяц.TERM=9,.6 мес.Это означает, что мы сможем накопить $1000, откладывая в конце каждого месяца $100 через 9 месяцев и 18 дней, если банковская ставка составит 10% годовых.Пусть мы найдем более рискованное предложение - банк со ставкой 20% годовых, а мы хотим накопить те же $1000. В этом случае TERM составит уже 9 месяцев Наконец, желая накопить те же $1000 мы рассчитываем вносить $200 в месяц в банк со ставкой 20% годовых. В этом случае TERM составит уже 4 месяца 24 дня.
|
TERM |
=NPER(D2/12;-D3;D4) |
=NPER(E2;-E3;;E4) |
=NPER |
=NPER |
||
|
Rate |
Ставка |
Ставка |
0,1 |
0,16 |
0,3 |
0,6 |
|
pmt |
пплат |
плт |
200 |
1000 |
100 |
200 |
|
pv |
бз |
бс |
1000 |
10000 |
4000 |
8000 |
|
NPER |
КПЕР |
КПЕР |
4,92 |
6,44 |
28,07 |
6,85 |
Предположим стоит задача накопить в банке сумму, которая через n месяцев составит определенное значение - FV (Future Value). Определим ее значение. Пусть в конце каждого месяца в банк вносится определенный платеж- PMT. Известна годовая ставка банковского процента - (i) и количество месяцев (n) на который мы ориентируемся.
Расчет FV выполняется по формуле:
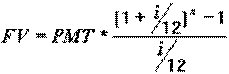
Пример. Пусть наш платеж в конце каждого месяца в течении полугода PMT=$500. Принимая банковскую ставку i=20% - (0.2), n=6 месяцев, имеем FV= $3128. Мы накопим только FV=$2502 ,если размер нашего ежемесячного платежа составит PMT=$400 при прочих равных условиях.
|
FV |
=FV(D2;D3;D4) |
=FV(E2/12;E3;E4) |
=FV(E2/12;E3;E4) |
=FV(G2;G3;G4) |
=FV(H2/12;H3;H4) |
||
|
Rate |
Ставка |
Ставка |
0,1 |
0,1 |
0,1 |
0,3 |
0,3 |
|
nper |
кпер |
кпер |
10 |
5 |
5 |
6 |
6 |
|
pmt |
выплата |
плт |
-1800 |
-1000 |
-1000 |
-300 |
-600 |
|
pv |
нз |
пс |
-500 |
||||
|
FV |
FV |
FV |
28687,36 |
5084,03 |
5605,21 |
3826,81 |
7653,62 |
Предположим мы рассчитываем регулярно, раз (в конце года) инвестировать сумму в валюте (РМТ) при известной норме банковской ставке (i) в процентах годовых в течении ряда периодов (n). Нас интересует величина инвестируемого капитала в данное время , для того чтобы решить, насколько это выгодно.
Например, должник предлагает выплатить долг в $5000 регулярными выплатами в два года по $2500 при существующей ставке 12% годовых в валюте. Имеется возможность получить с должника в настоящий момент сумму в $4500 сразу. Какой вариант предпочесть? Надо считать с помощью функции PV.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.