Использование электронных таблиц для расчета основных функций финансового менеджмента, страница 2

Другой пример. Предположим покупается новый автомобиль стоимостью $12000. Продавец предлагает кредит 7% в год с выплатой по $350 ежемесячно в течение 5 лет. Расчет показывает, что лучше сразу выплатить $12000, чем воспользоваться кредитом потому что потери в случае с кредитом свыше $5675, поскольку PV=$17675

Предположим покупается страховка стоимостью $60000, за которую в конце каждого месяца необходимо выплачивать $500 в течение 20 лет со ставкой на капитал 8% годовых. Является ли такой подход разумным?  PV=59777.146. Повидимому предложение о покупке страховки менее выгодное средство для инвестирования, поскольку теряем: $60000-$59777=$223. Расчет PV  выполняется по формуле:

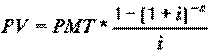
Пример.  PMT=$2000, i=12% - (0,12),  TERM=2года, PV=$3380

Предположим, имея первоначальный капитал в сумме PV мы хотим положить его на  депозит в банк для  накопления суммы, которая в будущем составит определенное значение - FV. Таким образом наша задача состоит в том, чтобы подобрать такой финансовый инструмент - банк, ценные бумаги, коммерческое предприятие, который обеспечил бы желательную нам ставку. Задан срок вложения капитала TERM- n. Необходимо сделать расчет ставки банковского процента, RATE -  (i), при которой будет накоплен капитал FV. Расчет RATE  выполняется по формуле:

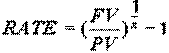
Пример. Пусть у Вас на руках сейчас $4000  (PV=$4000). Через 5  лет,  Вам понадобится $10000 (FV=$10000). Расчеты показывают, что размер искомой  годовой ставки на капитал должен составить:  RATE=20%

Чистый Дисконтируемый Доход (ЧДД) или NPV - Net Present Value - чистая стоимость в настоящее время:

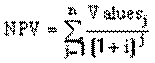
Здесь Values_{j -} значения денежных потоков - Cash Flow  в период  jпредставвляют собой результаты - эффекты, как, например, разность между доходами и расходами;

i -  дисконтная ставка на капитал;

n -  количество периодов. когда учитываются денежные потоки.

Принимается, что инвестиции, которые. как и затраты и представляют собой  денежные потоки размещаются равномерно и могут учитываться как в конце так и в начале каждого планируемого периода j .