|
n |
k |
t |
P(X) |
|
7 |
4 |
1 |
X3+X+1 |
|
15 |
11 |
1 |
X4+X+1 |
|
15 |
7 |
2 |
X8+X7+X6+X4+1 |
|
15 |
5 |
3 |
X10+X8+X5+X4+X2+X+1 |
|
31 |
26 |
1 |
X5+X2+1 |
|
31 |
21 |
2 |
X10+X9+X8+X6+X5+X3+1 |
Для декодирования сигналов БХЧ было разработано большое количество методов, требующих меньше памяти, чем прямой поиск в таблице. Одна из наиболее простых схем была предложена в работе [BERL80]. Ее основная идея состоит в вычислении полинома локализации ошибки с последующим нахождением его корней. Сложность данного алгоритма увеличивается как квадрат количества ошибок, которые нужно исправить.
Коды Рида-Соломона
Коды Рида-Соломона (Reed-Solomon codes — RS codes) — это широко используемый подкласс недвоичных кодов БХЧ. При использовании кодов Рида-Соломона данные обрабатываются порциями по m бит, именуемыми символами. Код (n,k) характеризуется следующими параметрами.
Длина символа m бит
Длина блока n = (2m – 1) символов = m(2m – 1) бит
Длина блока данных k символов
Размер контрольного кода n-k = 2t символов => m(2t) бит
Минимальное расстояние dmin = (2t+ 1) символов
Таким образом, алгоритм кодирования расширяет блок k символов до размера n, добавляя (n-k) избыточных контрольных символов. Как правило, m является степенью 2; широко используется значение m = 8.
Пример. Пусть t = 1, m = 2. Обозначая символы как 0, 1, 2, 3, их двоичные эквиваленты можно записать как 0 = 00; 1 = 01; 2 = 10; 3 = 11. Код имеет следующие параметры:
n = 22 – 1 = 3 символа = 6 бит,
n-k = 2 символа = 4 бит.
С помощью данного кода можно исправить любой пакет ошибок, который искажает 2-битовый символ.
Коды Рида-Соломона удобны для исправления пакетов ошибок. Данный тип кодов характеризуется высокоэффективным использованием избыточности, длина блоков и размеры символов могут легко приспосабливаться под сообщения разных размеров. Кроме того, для таких кодов существуют эффективные методы кодирования.
Чередование блоков
В беспроводных системах с блочными кодами широко используется метод чередования блоков; пример такого чередования приводится на рис. 8.8. Преимущество чередования состоит в том, что приемник распределяет пакет ошибок, исказивший некоторую последовательность битов, по большому числу блоков, благодаря чему становится возможным исправление ошибок. Чередование выполняется с помощью чтения и записи данных в различном порядке. На рис. 8.8 представлен простой и широко применяемый метод чередования. Здесь данные, которые необходимо передать, заносятся в прямоугольную матрицу, каждая строка которой состоит из n бит, что равно размеру блока, а считываются эти данные по столбцам. В результате k бит данных и соответствующие им (n-k) контрольных битов, которые вместе составляют блок из n бит, рассеиваются и перемешиваются с битами других блоков. После приема исходный порядок битов восстанавливается. Если во время передачи пакет помех воздействует на некоторую последовательность битов, то все эти биты оказываются разнесенными по различным блокам. Следовательно, от любой контрольной последовательности требуется возможность исправления лишь небольшой части от общего количества инвертированных битов. В частности, любой пакет ошибок длиной l = mb разбивается на m пакетов длиной b. После некоторого размышления легко понять справедливость такого утверждения. Предположим, что используется код (n,k), с помощью которого можно исправить все комбинации из t (или менее) ошибок; t = [(n-k)/2]. Если степень чередования равна m, то в результате будет получен код (mn, mk), с помощью которого можно исправить ошибки, затрагивающие до mt бит.
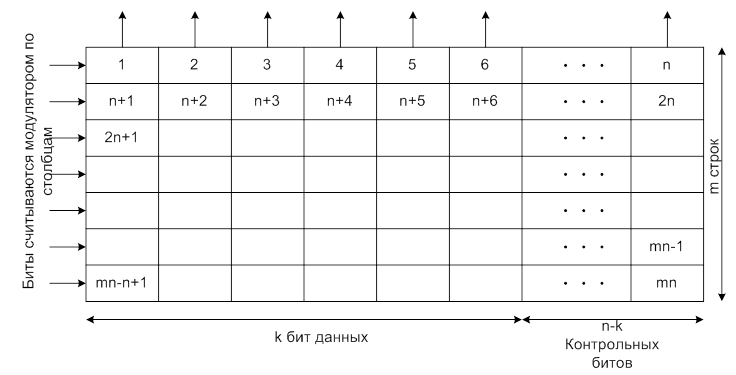
Рис.4 Чередование блоков
Примечание. Числа в ячейках матрицы указывают порядок считывании битов.
После чередования биты подаются на выход в следующем порядке: 1, n +1, 2n +1 и т.д.
Список литературы
1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.