Блочные коды с коррекцией ошибок, страница 4

     Необходимо отметить, что частота появления ошибок при коде со степенью 1/2 – это частота появления неисправленных ошибок , а E_b – энергия на один бит данных. Поскольку степень кодирования равна 1/2, каждому биту данных соответствуют  два канальных бита, следовательно удельная энергия кодированного бита в два раза меньше удельного бита данных, т.е. разница E_b/N₀  составляет 3дБ. Если рассмотреть удельную энергию кодированного бита такой системы, уровень битовых ошибок в канале составляет 2,4 х 10^-2, или 0,024.

В завершение необходимо отметить, что если значение E_b/N₀ – ниже определенного порогового, методы кодирования отрицательно сказываются на производительности системы. В примере, приведенном на рисунке, это пороговое значение равно приблизительно 5,4 дБ. При более низком значении E_b/N₀ использование дополнительных контрольных битов снижает удельную энергию битов данных, что ведет к увеличению числа ошибок. Если значение E_b/N₀ выше порогового, способность кода исправлять ошибки (эффективность кодирования) позволяет компенсировать снижение E_b и улучшить работу системы.

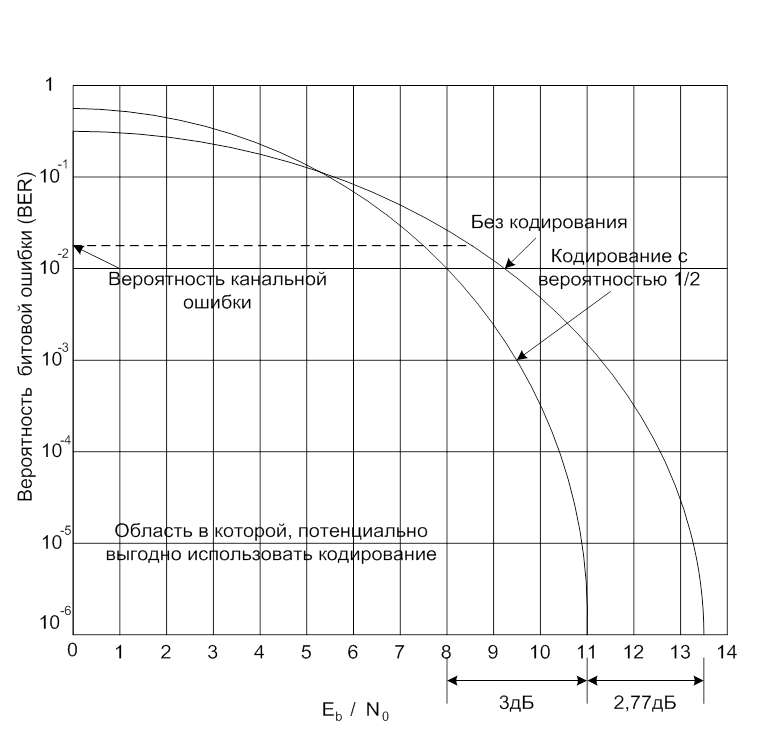
Рис. 2 Улучшение работы системы с помощью кодирования

Рассмотрим конкретные виды кодов с коррекцией ошибок.

Код Хэмминга

     Коды Хэмминга- это семейство блочных кодов с коррекцией ошибок (n,k), которые характеризуются следующими параметрами

 Длина блока                                               n=2^m-1

Количество битов данных                         k=2^m-m-1

Количество контрольных битов                n-k=m

Минимальное расстояние                           d_min=3

     Здесь m > 3. Коды Хэмминга просты в использовании и легко поддаются анализу, однако редко используются на практике. Рассмотрим этот тип кодов, чтобы проиллюстрировать на их примере некоторые фундаментальные принципы работы блочных кодов.

     Коды Хэмминга созданы для исправления 1- битовых ошибок. Для начала определим необходимую длину кода. Коды Хэмминга применяются также, как методы определения ошибок – в процессе кодирования сохраняются k бит данных и добавляются (n-k) контрольных битов. При декодировании используются две последовательности из (n-k) бит, одна из которых является кодовым словом входящего сигнала, а другая рассчитывается на основе полученных битов данных. Последовательности побитово сравниваются  с помощью логического исключающего ИЛИ. Результат сравнения называют синдромом. Биту синдрома присваивается значение 0, если биты двух последовательностей совпадают, и 1 – в противном случае.

     Синдром – это (n-k) – битовое слово в диапазоне от 0 до 2^(n-k)-1. Значение 0 свидетельствует об отсутствии ошибки . Если же ошибка присутствует, ее местоположение определяется из синдрома. Поскольку ошибочным может быть любой из k бит данных или (n-k) проверочных битов, должно выполнятся следующее соотношение:

    Приведенное уравнение определяет количество битов, необходимое для исправления 1- битовой ошибки в слове, содержащем k бит данных. В таблице приводится число контрольных битов, необходимое для последовательностей данных разной длины.

Таблица 1  Требования к кодам Хэмминга

 Для удобства генерируемый синдром должен обладать следующими свойствами:

• Если синдром состоит только из нулей – ошибки не обнаружены.

• Если один и только один бит синдрома равен 1 – ошибка присутствует в одном из контрольных битов; в этом случае исправлять ошибку не нужно.