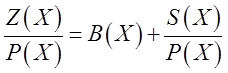Блочные коды с коррекцией ошибок, страница 7

                                                                     ●

где В(Х) — частное, a S(X) — остаток деления. Следовательно, S(X) является функцией Z(X). Каким же образом полученный результат можно использовать для исправления ошибок? Для ответа на этот вопрос, запишем уравнение ● в развернутой форме:

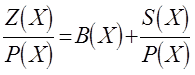
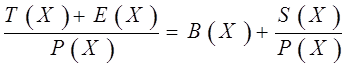
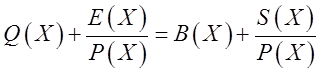
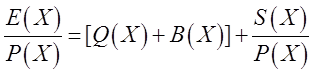
     Видим, что деление Е(Х)/Р(Х) дает тот же остаток, что и Z(X)/P(X). Следовательно, значение синдрома S(X) зависит только от ошибочных битов и не зависит от начальной последовательности битов (переданного значения Т(Х)). Если ошибоч­ные биты Е(Х) можно получить из синдрома S(X), то ошибки в Z(X) можно испра­вить посредством простого сложения:

Z(Х) + Е(Х) = T(Х) + Е(Х) + Е(Х) = Т(Х).

     Поскольку S(X) зависит только от Е(Х), возможности блочного цикличе­ского кода определить очень легко. Синдром состоит из (n-k) бит, следова­тельно, он может принимать 2^n-k  возможных значений. Нулевой синдром указывает на отсутствие ошибок. Следовательно, всего можно исправить (2^n-k - 1) различных ошибочных комбинаций. Чтобы с помощью кода (n,k) мож­но было исправить все возможные однобитовые ошибки, должно выполнять­ся неравенство n<(2^n-k - 1). Исправление всех 1- и 2- битовых ошибок требует выполнения следующего неравенства:

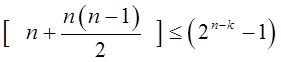
Способ получения Е(Х) из S(X) может зависеть от используемого кода. Наи­более простой подход — построить таблицу, которая ставила бы в соответствие значениям Е(Х) значения S(X). После этого потребуется простой способ выполне­ния поиска в такой таблице.

Коды БХЧ

Коды БХЧ являются одним из наиболее мощных циклических блочных кодов и получили широкое применение в беспроводных приложениях. Для любой пары положительных целых чисел m и t существуют двоичные коды БХЧ (n, к) со сле­дующими параметрами.

Длина блока                                        n = 2^m - 1

Количество контрольных битов       n-k < mt

Минимальное расстояние        _   d_min  > 2t + 1

С помощью такого кода можно исправить все слова, содержащие t (или менее) ошибок. Порождающий многочлен кода БХЧ можно создать из множителей по­линома (X^2m-1 + 1). Использование кодов БХЧ предоставляет некоторую свободу выбора параметров (длина блока, степень кодирования). В табл. 8.4 перечислены  параметры БХЧ для кодов длиной до 2⁸ - 1. В табл. 8.5 приводятся некоторые порождающие многочлены БХЧ.

Таблица 3  Параметры кодов БХЧ

Таблица 4 Порождающие многочлены кодов БХЧ