Блочные коды с коррекцией ошибок, страница 3

    В блочном коде (n,k) имеется 2^k приемлемых кодовых слов из 2ⁿ возможных. Отношение числа избыточных битов к числу битов данных (n-k)/k принято называть избыточностью кода; отношение количества битов данных к пол­ному числу битов (k/n) называют степенью кодирования. Степень кодиро­вания — это мера того, какая дополнительная полоса потребуется после кодирова­ния, если скорость передачи данных мы хотим сохранить такой же, какая была до кодирования. Например, при степени кодирования 1/2 для сохранения скорости пе­редачи системе потребуется полоса, в два раза большая, чем та, которая необходима для передачи некодированного сигнала. Для рассмотренного выше примера степень кодирования равна 2/5, следовательно, для сохранения скорости передачи потребу­ется увеличить ширину полосы в 2,5 раза. Т.е. если скорость передачи сигнала на входе кодера равна 1 Мбит/с, то для сохранения прежних параметров скорость вы­ходного сигнала должна быть равна 2,5 Мбит/с.

     Для кода, состоящего из кодовых слов w₁, w₂, .... w_s, где s = 2ⁿ, минимальное расстояние кода d_min определяется следующим образом:

d_min=min[d(w_i, w_j)]

Можно показать, что если для кода выполняется неравенство d_min > 2t + 1 (t — некото­рое положительное целое число), то с помощью данного кода можно исправить все символы, содержащие до ( t-1)ошибочных битов, включительно. Если d_min > 2t, то можно исправить все символы, содержащие до (t—1) ошибочных битов. Кроме того, будут обнаружены все символы с t ошибочными битами, исправить которые, в общем слу­чае, нельзя. Верно и обратное утверждение — каждый код, позволяющий исправ­лять до t ошибочных битов, должен удовлетворять условию d_min>2t + l. Для каждого кода, позволяющего исправлять до (t-1) ошибочных битов и обнаруживать все сим­волы с t ошибками, должно выполняться условие d_min >2t.

     Связь между d_min и t можно записать другим способом, выразив максималь­ное количество битовых ошибок в кодовом слове, гарантированно исправляемых кодом, в таком виде:

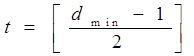
где [x] — наибольшее целое число, не превышающее х (например, [6,3] = 6). Более то

го), если нас интересует только обнаружение ошибок, но не их исправление, коли­чество обнаруживаемых ошибок t удовлетворяет следующему равенству:

t = d_min-1

     Последнее выражение можно понять интуитивно, если вспомнить, что d_min битовых ошибок может изменить одно конкретное кодовое слово на другое. При любом меньшем количестве ошибок этого произойти не может.

Выбирая блочный код, нужно учитывать следующие соображения.

 1.При данных n и k предпочтительным является максимально возможный d_min.

 2. Код должен быть сравнительно простым для кодирования и декодирования, требуя минимальной памяти и времени обработки.

 3. Для уменьшения ширины требуемой полосы число избыточных битов (n-k) должно быть небольшим.

4. Для снижения уровня ошибок число избыточных битов (n-k) должно быть   большим.

Очевидно, что два последних требования противоречат друг другу, так что нужно выбирать некоторый компромиссный вариант.

Перед тем как перейти к рассмотрению примеров кодов, обратимся к рис. 8.6. Графики подобного типа довольно часто приводятся в литературе для демонстрации эффективности разных схем кодирования (кодирование может использоваться для снижения необходимого значения E_b/N₀, что позволяет достичь заданного уровня битовых ошибок) Кодирование ,которое мы рассматриваем влияет на отношение E_b/N₀.  На рис. 8.6 кривая справа соответствует системе модуляции без кодирования; в затененной области параметры системы могут быть улучшены. В этой области при заданном E_b/N₀ достигается меньшее значение BER.Верно и  обратное утверждение —   при заданном ВЕR требуется меньшее значение E_b/N₀. Кривая, расположенная левее, представляет собой типичный результат обработки сигнала кодом со степенью кодирования 1/2 ( в этом случае число битов данных равно числу контрольных битов). Для частоты возникновения ошибок 10^-5 использование  кодирования позволяет снизить E_b/N₀ на 2,77 дБ. Это улучшение называется эффективностью кодирования. Эффективность кодирования — это снижение необходимого уровня E_b/N₀ для системы с кодированием по сравнению с системой без кодирования (подразумевается одна и та же модуляция) для достижения заданной частоты ошибок.