












Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Кафедра «Теоретическая и прикладная механика»
РАСЧЁТ ПЛОСКИХ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ФЕРМ
Методические указания к выполнению контрольной работы
по строительной механике
Комсомольск-на-Амуре 2007
УДК 624.04
Расчёт плоских статически определимых ферм: Методические указания к выполнению контрольной работы по строительной механике /Сост.: В.С. Симонов. – Комсомольск-на -Амуре: Комсомольский-на Амуре государственный технический университет, 2007. – 14 с.
Даны краткие методические указания к расчёту простых статически определимых плоских ферм на постоянную и временную нагрузки. Приведен пример решения задачи с необходимыми пояснениями.
Печатается по постановлению редакционно-издательского совета Комсомольского-на-Амуре государственного технического университета.
Согласовано с отделом стандартизации.
Рецензент Г.С. Лейзерович
1. Общие методические указания
Расчёт плоских статически определимых ферм в рамках задания [1] включает: а) аналитическое определение внутренних усилий от постоянной нагрузки в стержнях только одной панели; б) построение линий влияния внутренних усилий в тех же стержнях и определение с их помощью максимальных и минимальных значений расчётных усилий при невыгодном сочетании постоянной и временной нагрузок.
В строительных сооружениях внешняя нагрузка передаётся в узлы фермы через различные конструктивные элементы, например, плиты покрытий, настилы, поперечные балки и др. Это позволяет практически исключить деформацию изгиба стержней фермы при жёстком их соединении в узлах, а при расчёте использовать расчётную схему с шарнирным соединением стержней в узлах, хотя в реальных фермах стержни соединены жёстко.
Аналитическое определение внутренних усилий в стержнях простых ферм и построение линий влияния основано на использовании уравнений статического равновесия для условно отсечённой части фермы (метод сечений). В зависимости от того, как проведено секущее сечение, и какая часть фермы рассматривается, различают способ вырезания узлов и способ простых сечений.
Вспособе вырезания узлов сечение проводят
так, чтобы рассекались все стержни, сходящиеся в одном узле. Условно вырезанный
узел с внешней силой (если она имеется) и внутренними усилиями в рассечённых
стержнях (продольными силами) представляет плоскую систему сил, сходящихся в одной
точке, для которой можно составить только два уравнения
равновесия вида, ![]()
![]() где X и Y любые, не обязательно взаимно перпендикулярные,
оси координат. Соответственно, на момент рассмотрения данного узла число
неизвестных усилий в нём не должно быть больше двух. Поэтому требуется
устанавливать определённый порядок вырезания узлов и последовательно определять
усилия в стержнях всех предыдущих узлов.
где X и Y любые, не обязательно взаимно перпендикулярные,
оси координат. Соответственно, на момент рассмотрения данного узла число
неизвестных усилий в нём не должно быть больше двух. Поэтому требуется
устанавливать определённый порядок вырезания узлов и последовательно определять
усилия в стержнях всех предыдущих узлов.
Простое сечение – это сечение, условно рассекающее ферму на две части пересечением не более трёх стержней, входящих в разные узлы. В этом случае одна из частей фермы содержит три неизвестных усилия в рассечённых стержнях и внешние силы в узлах. Для плоской системы сил, не сходящихся в одной точке, можно составить три независимых уравнения равновесия, в каждое из которых входит только лишь одно неизвестное усилие.
Если из трёх рассечённых стержней два параллельны
между собой, то составляют уравнения равновесия вида: ![]() где
где
![]() – ось координат, перпендикулярная
двум параллельным неизвестным усилиям, 1,2 – точки пересечения двух
пар неизвестных непараллельных усилий, так называемые моментные точки.
– ось координат, перпендикулярная
двум параллельным неизвестным усилиям, 1,2 – точки пересечения двух
пар неизвестных непараллельных усилий, так называемые моментные точки.
При произвольной ориентации трёх рассечённых
стержней составляют уравнения равновесия вида, ![]() где 1,2,3 – точки пересечения трёх пар
непараллельных неизвестных усилий.
где 1,2,3 – точки пересечения трёх пар
непараллельных неизвестных усилий.
Следует заметить, что каждый из названных способов имеет свои преимущества и свои недостатки, и обычно их применяют во взаимном сочетании, что и иллюстрируется в рассматриваемом ниже примере.
2. Пример расчёта простой фермы
Для фермы, расчётная схема которой представлена на рисунке 1, требуется:
а) аналитически определить усилия во всех стержнях четвёртой панели, считая слева, от постоянной погонной нагрузки qП;
б) построить линии влияния усилий в тех же стержнях;
в) загрузить линии влияния постоянной нагрузкой и сравнить результаты аналитическим определением усилий;
г) определить максимальные и минимальные значения расчётных усилий в рассматриваемых стержнях при невыгодных сочетаниях постоянной и временной нагрузки qВс помощью линий влияния.
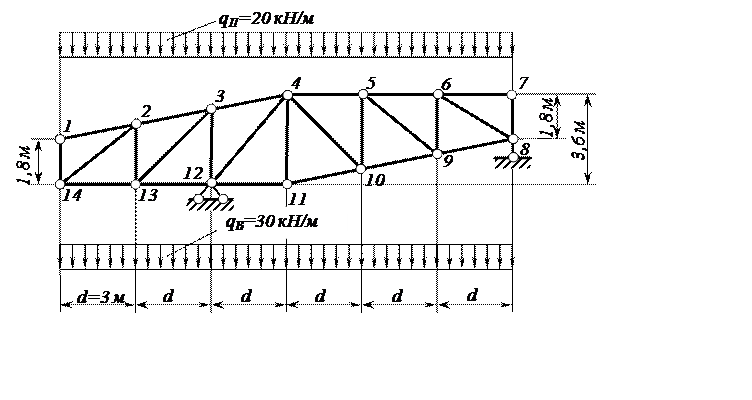

Рисунок 1 – Расчётная схема фермы
Замечание. В отличие от задания, содержащегося в [1], в нашем примере в состав постоянной нагрузки входит погонная нагрузка qП , приложенная к узлам верхнего грузового пояса, а временная погонная нагрузка qВ приложена к узлам нижнего пояса. Это сделано с целью, чтобы показать особенности определения усилий с помощью линий влияния в стержнях четвёртой панели 4-11 и 5-10, неодинаково работающих при загружении верхнего или нижнего грузового поясов.
2.1. Аналитический расчёт на постоянную нагрузку.
2.1.1. Определяем реакции опор.
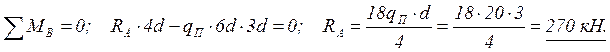
![]()
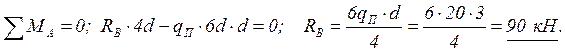
Проверка:
![]()
т.е. реакции определены правильно.
2.1.2. Приводим погонную постоянную нагрузку qП в узлы верхнего пояса.
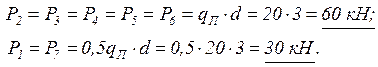
Расчётная схема фермы при этом примет вид:
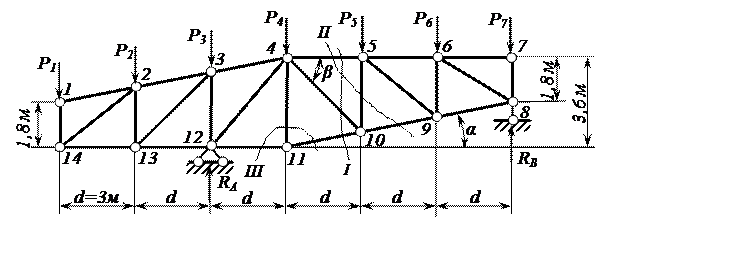
Рисунок 2 – Расчётная схема фермы с узловой постоянной нагрузкой
2.1.3. Усилия в стержнях четвёртой панели находим с помощью простых сечений I, II и вырезанием узла 11 сечением III.
Тригонометрические функции углов наклона стержней:
![]()
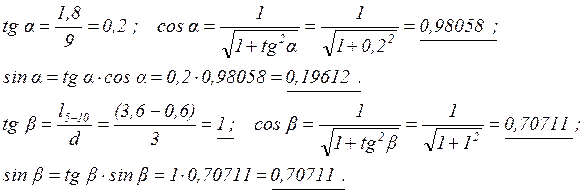
2.1.4. Определяем усилия в стержнях, рассекаемых простым сечением I, из условий равновесия правой отсечённой части фермы (рис. 3).
Две моментные точки находятся в узлах 4 и 10; третья моментная точка К находится на пересечении линий действия усилий N5-4и N10-11 на расстоянии c от правой опоры.
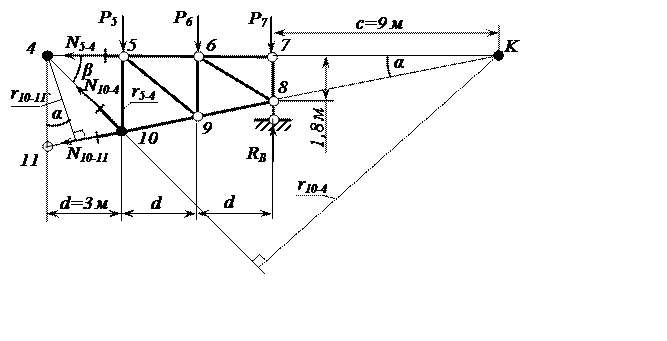
Рисунок 3 – Правая часть фермы, отсечённая сечением I
Плечи усилий N10-11, N5-4 и N10-4относительно моментных точек равны, соответственно:
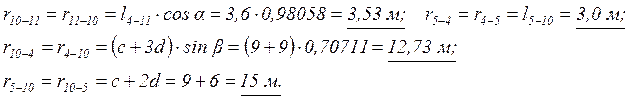
Здесь 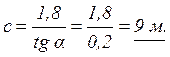
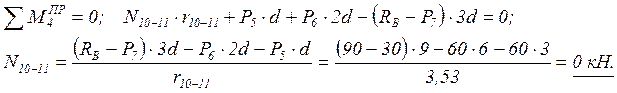
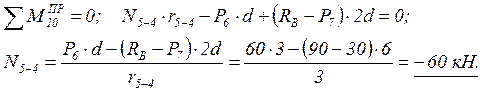
![]()
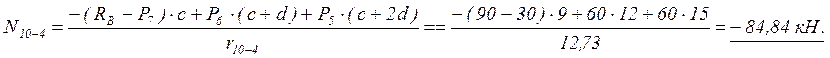
![]() 2.1.5. Определяем усилие в стержне 5-10,
рассекаемом простым сечением II, из условия равновесия правой отсечённой части фермы
(рисунок 4).
2.1.5. Определяем усилие в стержне 5-10,
рассекаемом простым сечением II, из условия равновесия правой отсечённой части фермы
(рисунок 4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.