Предположим, что температура стержня одинакова во всех точках, атмосферным давлением можем пренебречь и объемные силы отсутствуют. Существует только одно внешние воздействие, а именно изгибающий момент М, которые будут действовать, в одной из главных плоскостей двумя равными и противоположными моментами М. Определим начало координат в центре тяжести поперечного сечения, а плоскость xz — в главной плоскости изгиба.
В теории упругости уже известно аналитическое решение для балки, воспользуемся основными формулами и соотношениями для решения.
Закрепим балку жестко на левом торце (исключим перемещения вдоль осей Z и X), и исключим изгиб в плоскости YZ, к правому торцу приложим изгибаю момент.
Рассмотрим искомое решение для напряжений в виде:
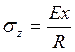 ,
,
![]()
Где R – радиус кривизны стержня после изгиба.
Это решение удовлетворяет граничным условиям.
Оно также удовлетворяет и условиям равновесия:
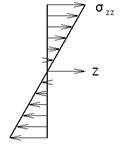
![]() (i,j=1,2,3)
(i,j=1,2,3)
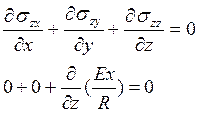
Таким
образом, мы имеет распределение напряжений в виде 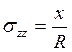 , остальные
σij=0 .
, остальные
σij=0 .
Связи напряжений и деформаций, вытекающая из закона Гука, имеет вид:
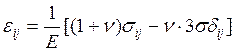
![]()
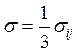
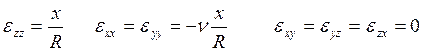
И наконец, рассмотрев формулу
Коши: 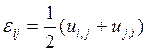 можем записать следующие выкладки:
можем записать следующие выкладки:
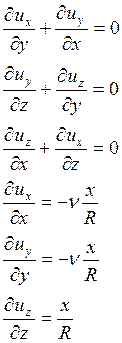
Изгибающий момент М определяется формулой
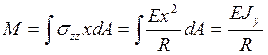
в которой ![]() - момент инерции поперечного сечения балки
относительно нейтральной оси, параллельной оси у,R – радиус кривизны стержня после изгиба.
- момент инерции поперечного сечения балки
относительно нейтральной оси, параллельной оси у,R – радиус кривизны стержня после изгиба.
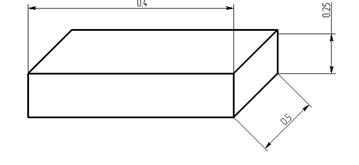
Предсталю решение данной задачи в MSC.Patran, Nastran. Стержень имеет размеры 1x1x10 мм, модуль упругости Е = 7000 кГ/мм2, коэффициент Пуассона v = 0.3, радиус кривизны стержня после изгиба R = 10 мм.
2. Основные параметры расчета и создания модели.
В последние годы метод конечных элементов стал одним из наиболее популярных численных методов решения краевых задач механики сплошных сред. Наличие нерегулярных границ в большинстве практических задач не позволяет построить аналитическое решение дифференциальных уравнений, и численные методы стали единственно возможным средством получения достаточно точных и подробных результатов. Подход метода конечных элементов состоит в разбиении тела на элементы конечных размеров; чем больше эти элементы, тем лучше с точки зрения минимизации числа получающихся уравнений. Поведение каждого элемента приближенно воспроизводит поведение малой области тела, которую он представляет, между элементами налагается условие непрерывности. Благодаря своей эффективности и сравнительной легкости, с которой могут быть учтены реальные граничные условия, метод достиг высокого уровня развития и диапазона применимости.
Будем решать нашу задачу в предположении о малости деформаций, поворотов и перемещений. То есть рассмотрим задачу в геометрически линейной постановке.
Приведем основные соотношения МКЭ в виде матриц:
- функция перемещения:
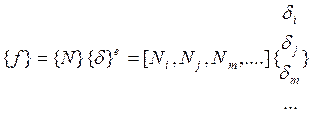 ,
где N – матрица функции,
,
где N – матрица функции, ![]() - вектор узловых
перемещений.
- вектор узловых
перемещений.
- функция деформации:
![]()
- функция напряжения:
![]()
Где ε0, σ0, - начальные деформации и напряжения.
D – матрица упругости.
- матрица упругости :
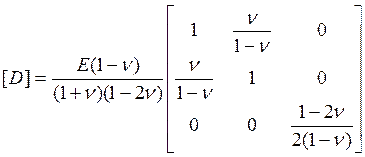
- матрица жесткости:
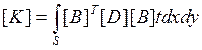
Если толщина t
постоянная, то в следствии постоянности матриц можем произвести интегрирование:
![]() .
.
Следует отметить, что постепенно задача сводиться к решению системы линейных алгебраических уравнений с постоянной матрицей жесткостью.
МКЭ будет реализован с помощью пакета MSC. Nastran. Непосредственную подготовку (построение модели, разбиение, задание свойств, граничных условий и нагрузок) будем производить в пакете MSC. Patran.
 |
 |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.