Определение перемещений в плоских статически неопределимых стержневых системах: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика"

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Кафедра «Механика и анализ конструкций и процессов»

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В ПЛОСКИХ

СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ

СИСТЕМАХ

Методические указания к выполнению контрольной и расчётно-проектировочной работы по строительной механике

Комсомольск-на-Амуре 2010

УДК 624.04

 

Определение перемещений в плоских статически неопределимых стержневых системах: Методические указания к выполнению контрольной и расчётно-проектировочной работы по строительной механике / Сост. В.С. Симонов, М.Р. Петров – Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2010. – 12 с.

В методических указаниях рассматриваются особенности определения перемещений в статически неопределимых стержневых системах на примере простейшей статически неопределимой балки и даются рекомендации по реализации метода определения перемещений в статически неопределимых стержневых системах с помощью интегралов Мора.

Приведены примеры определения перемещений в статически неопределимой балке и раме. Решение примеров сопровождается необходимыми рисунками и комментариями.

Методические указания предназначены для студентов заочной и дневной форм обучения, изучающих курс «Строительная механика».

Печатается по постановлению редакционно-издательского совета ГОУВПО «Комсомольский-на-Амуре государственный технический университет».

Согласовано с отделом менеджмента качества

Рецензент Г.С. Лейзерович

ВВЕДЕНИЕ

Обращаясь к теории определения перемещений в упругих стержневых системах [1, 3], заметим, что в ней не оговаривается, является система статически определимой или статически неопределимой. Достаточно знать грузовое состояние стержневой системы (для балок и рам – грузовую эпюру изгибающих моментов М_Р – от заданной нагрузки) и так называемые единичные состояния той же системы, соответствующие искомым перемещениям.

Например, необходимо определить прогиб Δ_1Р статически неопределимой балки под силой Р и угол поворота сечения Δ_2Р правого шарнирно опёртого конца (рисунок 1,а).

На основании общего принципа и правил определения перемещений в стержневых системах с помощью интегралов Мора прогиб Δ_1Р и угол поворота Δ_2Р получим, вычисление которых выполняется «перемножая» эпюру изгибающих моментов в статически неопределимой балке М_Р (рисунок 1,б) – от заданной внешней нагрузки на так называемые единичные эпюры изгибающих моментов  и  (рисунок 1,в,г) –от условных единичных «нагрузок»  и , соответственно, в той же статически неопределимой балке.

Эти эпюры для рассматриваемых состояний статически неопределимой балки приведём из справочных данных [2,3,5] как известные решения.

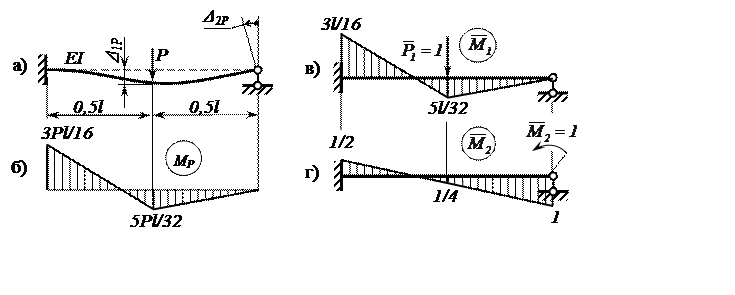
Рисунок 1 –Грузовое и единичные состояния статически

неопределимой балки

Если бы готовых решений для этих состояний не было, то пришлось бы трижды раскрывать статическую неопределимость: от заданной нагрузки «Р», идентично – единичного состояния от  и единичного состояния от .

В соответствии с общим правилом искомые перемещения (вычисление интегралов Мора путём перемножения соответствующих эпюр) в этом случае выполним, используя готовые формулы перемножения [1,2,3]:

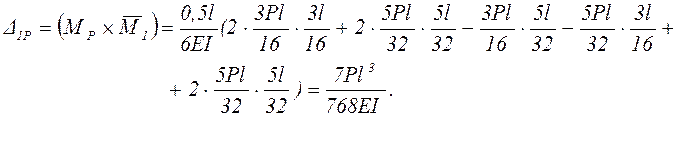
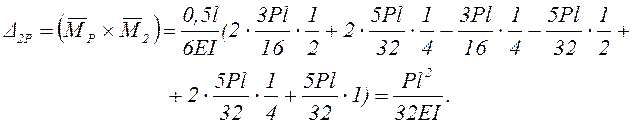
Решение поставленной задачи существенно упрощается, если учесть, что при правильном раскрытии статической неопределимости любой вариант эквивалентной системы метода сил имеет те же перемещения, что и заданная статически неопределимая система. Но эквивалентная система (основная система, загруженная заданной внешней нагрузкой и усилиями в устранённых «лишних» связях) статически определима, значит единичные состояния, соответствующие определяемым перемещениям, можно рассматривать в любом варианте основной системы метода сил.

Покажем на примере той же статически неопределимой балки, что одинаковые значения перемещений Δ_1Р и Δ_2Р получим при различных вариантах основной системы метода сил.

Для первого варианта основной системы эквивалентное грузовое и единичные состояния представлены на рисунке 2.

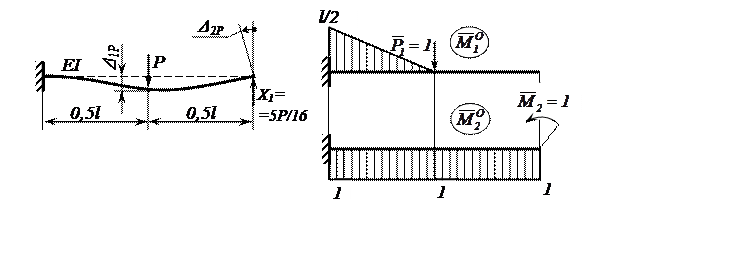
Рисунок 2 – Эквивалентное грузовое и единичные состояния 1-го

варианта основной системы

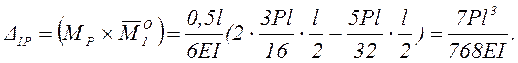
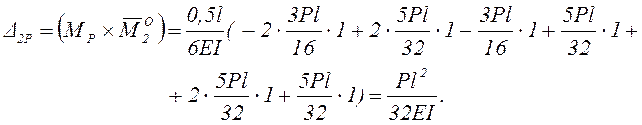
Для второго варианта основной системы эквивалентное грузовое и единичные состояния представлены на рисунке 3.

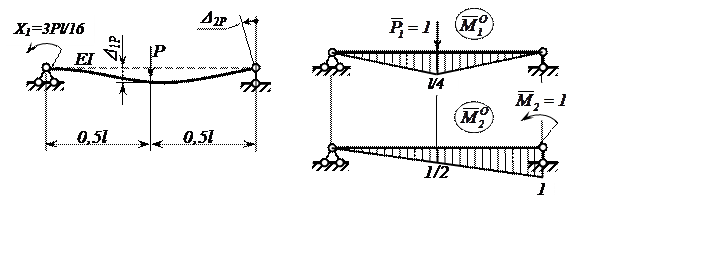
Рисунок 3 – Эквивалентное грузовое и единичные состояния 2-го

варианта основной системы

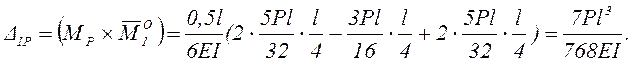
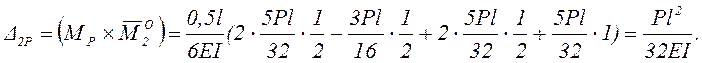Для третьего варианта основной системы эквивалентное грузовое и единичные состояния представлены на рисунке 4.

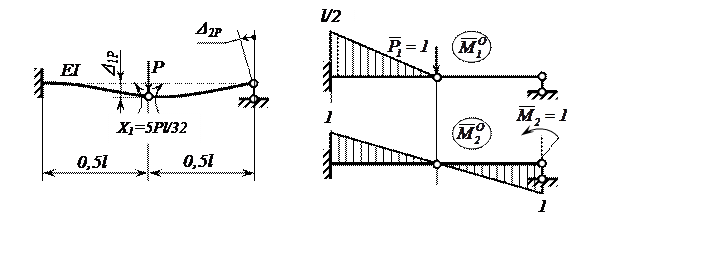
Рисунок 4 – Эквивалентное грузовое и единичные состояния 3-го

варианта основной системы

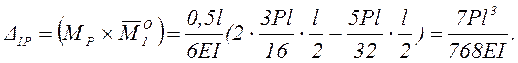
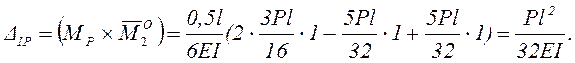
Таким образом, при использовании любого варианта основной системы метода сил при правильном раскрытии статической неопределимости получаем одни и те же значения перемещений, т.е. расчётчику предоставляется возможность выбрать тот вариант основной системы, при котором вычисления будут наиболее простыми, с меньшими затратами времени.

ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ В ПЛОСКИХ

СТАТИЧЕНСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМАХ

Пример 1. Определить прогибы посередине пролетов АВ, ВС и угол поворота сечения над опорой В статически неопределимой балки (рисунок 5).

Рисунок 5 – Расчётная схема балки

Решение выполняем в следующей последовательности.

1. Раскроем статическую неопределимость балки методом сил.

Методика раскрытия статической неопределимости методом сил рассматривается в методических указаниях [4], поэтому здесь подробных комментариев к раскрытию статической неопределимости не приводим.

Необходимые расчётные схемы и соответствующие эпюры изгибающих моментов представлены на рисунке 6.