Определение перемещений в плоских статически неопределимых стержневых системах: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 2

Уравнение метода сил для один раз статически неопределимой балки

 и  вычислим, перемножая соответствующие эпюры изгибающих моментов по правилу Верещагина.

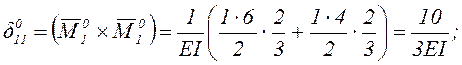
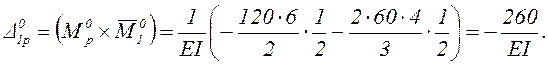
Х₁ – изгибающий момент в поперечном сечении балки над опорой В найдём из уравнения метода сил:

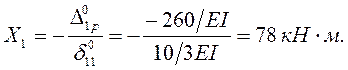
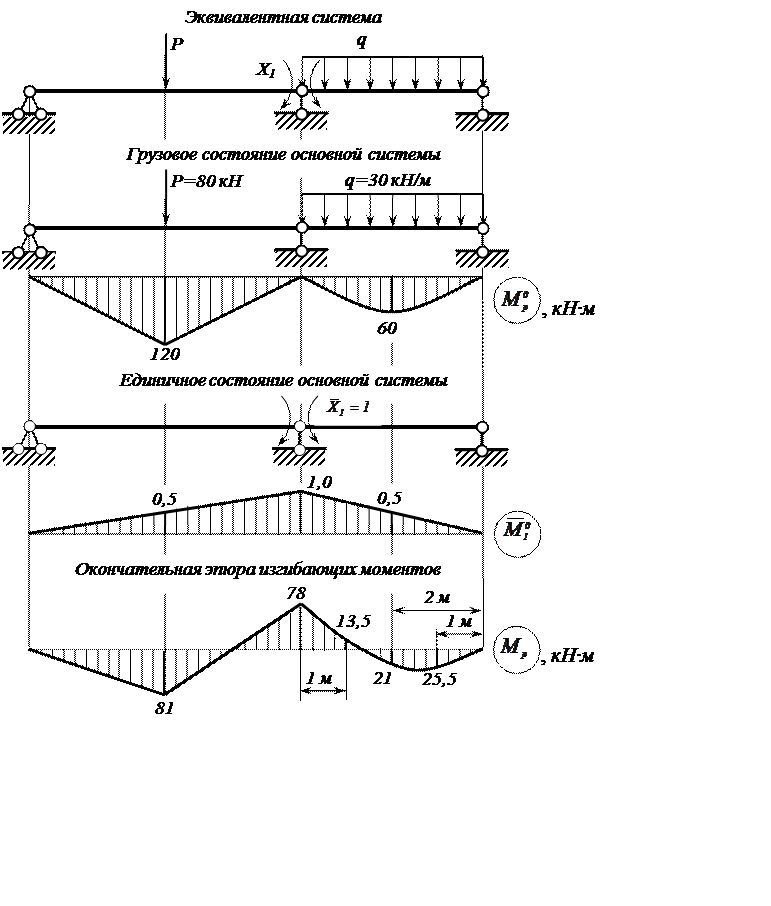
Рисунок 6 – Расчётные схемы и эпюры изгибающих моментов

к раскрытию статической неопределимости балки

Эпюру изгибающих моментов в заданной статически неопределимой балке (так называемую окончательную эпюру М_р ) получим, суммируя эпюру  с «исправленной» единичной эпюрой .

Выполняем деформационную проверку решения, подтверждающую, что взаимный угол поворота поперечных сечений в эквивалентной системе над опорой В отсутствует, т.е выполняется условие эквивалентности в методе сил.

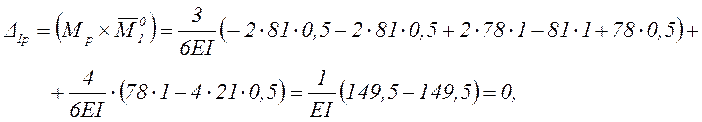
Перемножение эпюр здесь выполнено по готовым формулам.

2. Для определения заданных прогибов , и угла поворота  сечения В строим эпюры изгибающих моментов в той же основной системе метода сил от единичных сил и единичного момента , соответственно, при этом эпюру построим для двух вариантов третьего единичного состояния.

Для удобства перемножения эпюр расположим эпюру М_р и соответствующие единичные эпюры на одном рисунке 7.

3. Прогибы и угол поворота найдём, «перемножая» эпюру М_р  на эпюры .

Перемножение эпюр выполним здесь по готовым формулам, поэтому на всех эпюрах пролёта ВС с равномерно распределённой нагрузкой приведём значения посередине соответствующих участков.

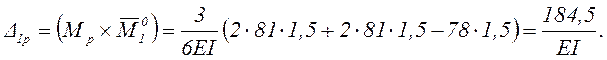
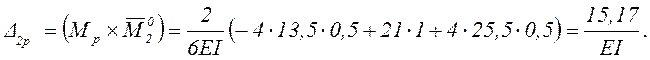
Используя 1-й вариант третьего единичного состояния, получим

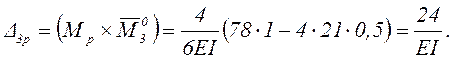
Для 2-го варианта третьего единичного состояния

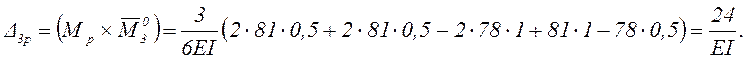
Получен тот же результат, что и для 1-го варианта, что лишний раз подтверждает правильность раскрытия статической неопределимости.

Положительные значения перемещений , , указывают, что они направлены в сторону единичных сил ,  т.е. вниз, а  – в сторону единичного момента , т.е. против хода часовой стрелки.

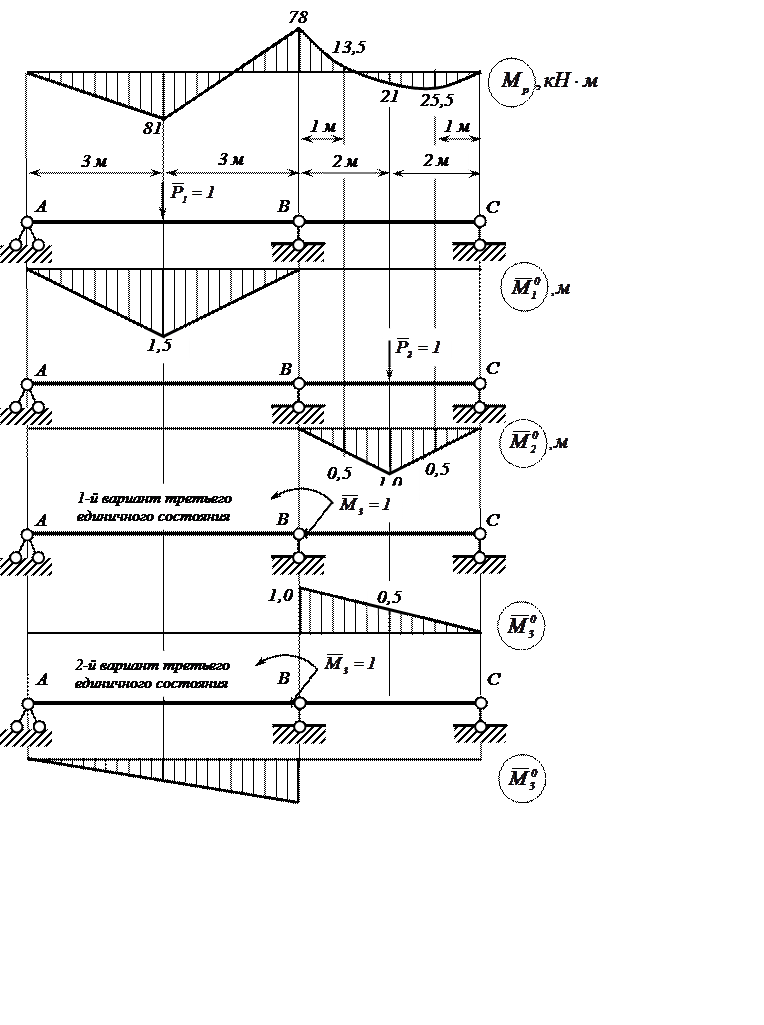Рисунок 7 – Эпюры изгибающих моментов грузового состояния

статически неопределимой балки и единичных состояний основной системы

Пример 2. Определить возможные перемещения узлов (линейные и угловые) статически неопределимой рамы (рисунок 8).

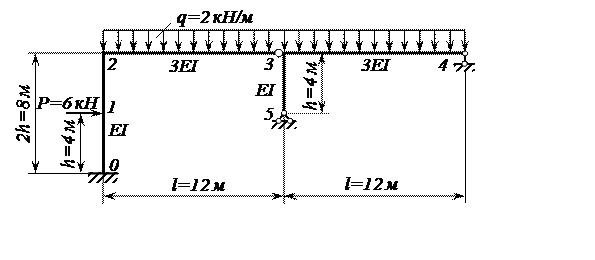
Рисунок 8 – Расчётная схема статически неопределимой рамы

Анализируя типы опорных связей и способы их наложения, видим, что жёсткие узлы рамы 2 и 3 могут поворачиваться независимо друг от друга и перемещаться в горизонтальном направлении на одну и ту же величину.

Обозначим угловые перемещения: узла 2 – Δ_1Р, узла 3 – Δ_2Р и линейное горизонтальное перемещения этих узлов – Δ_3Р.

В результате раскрытия статической неопределимости этой рамы методом сил [4] была получена эпюра изгибающих моментов грузового состояния М_Р (рисунок 9). Правильность решения подтверждена деформационной проверкой, в основе которой – определение перемещений в эквивалентной статически определимой системе.

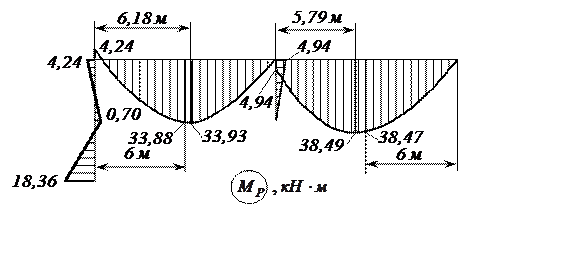
Рисунок 9 – Эпюра изгибающих моментов грузового состояния М_Р

Для определения перемещений Δ_1Р, Δ_2Р, Δ_3Р используем ту же основную систему метода сил, что и при раскрытии статической неопределимости.

Единичное состояние основной системы, соответствующее углу поворота Δ_1Р, представлено на рисунке 10.

Угловое перемещение узла 2

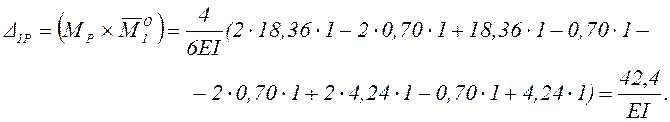
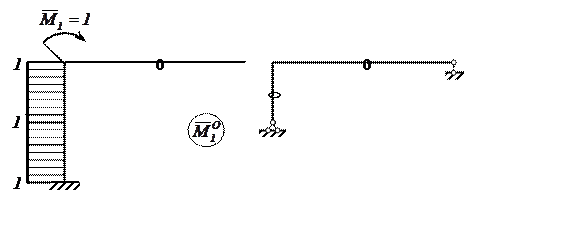
Рисунок 10 – Единичное состояние основной системы

для определения Δ_1Р

Единичное состояние основной системы, соответствующее углу поворота Δ_2Р, представлено на рисунке 11.

Угловое перемещение узла 3

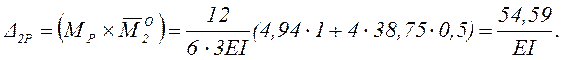
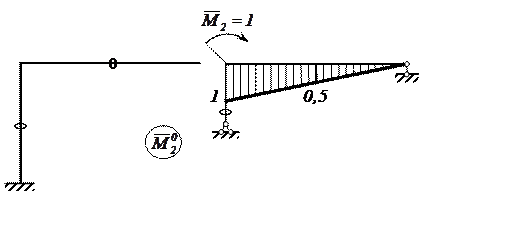
Рисунок 11 – Единичное состояние основной системы

для определения Δ_2Р

Линейное перемещение Δ_3Р узлов 2 и 3 найдём, рассматривая два варианта единичного состояния, прикладывая  в узле 2 (рисунок 12) и в узле 3 правой части основной системы (рисунок 13).

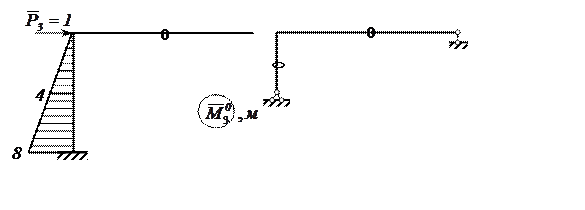
Рисунок 12 – 1-й вариант единичного состояния основной системы для определения Δ_3Р

В этом случае получим:

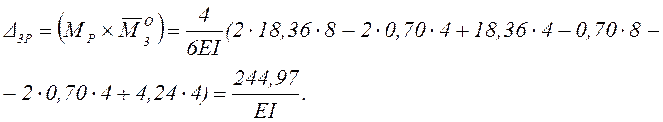
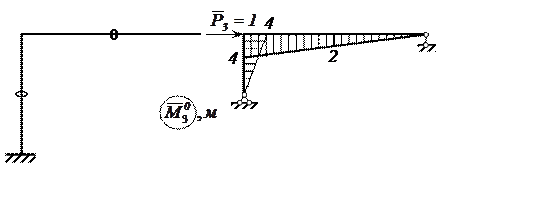
Рисунок 13 – 2-й вариант единичного состояния основной системы для определения Δ_3Р

Используя этот вариант эпюры , получим::

Незначительное расхождение значений Δ_3Р при двух вариантах  3-го единичного состояния объясняется вычислительной погрешностью, обусловленной принятой точностью представления значений эпюры М_Р.

Относительная «невязка» полученных значений составляет

.

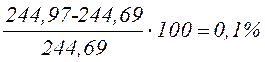Если принять большую точность – до пяти значащих цифр (что в инженерных расчётах излишне), то расхождение значений будет ещё меньше.

Как увидим далее, такие же значения перемещения получим при расчёте этой же рамы методом перемещений [5], в котором за неизвестные принимаются именно перемещения узлов:

Z₁=42,353/EI=Δ_1P;  Z₂=54,588/EI=Δ_2P;  Z₃=244,706/EI=Δ_3P.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Дарков, А.В. Строительная механика: учебник для вузов / А.В. Дарков,

Н.Н. Шапошников. – 9-е изд., испр. – СПб. Лань, 2004. – 655 с.

2. Руководство к практическим занятиям по курсу строительной механики: Статика стержневых систем. Учеб. пособие для строит спец. вузов / Под общ. ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1980, – 384 с.

3. Определение перемещений в плоских статически определимых стержневых системах: Методические указания по курсу «Строительная механика» / Сост. В.С. Симонов, С.В. Макаренко. – Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2009. – 19 с.

4. Расчёт статически неопределимых плоских рам методом сил: Методические указания по курсу «Строительная механика» / Сост. В.С. Симонов, Г.С. Лейзерович – Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2009, – 17 с.

5. Расчёт статически неопределимых плоских рам методом перемещений: Методические указания по курсу «Строительная механика» / Сост. В.С. Симонов, Г.С. Лейзерович – Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2009, – 17 с.