Определение деформации трубы

Деформация трубы определяется тремя компонентами: продольным удлинением , тангенциальным удлинением  и углом сдвига , так как сдвиги, а  можно определить из условия несжимаемости:

Таким образом, сам тензор деформаций является девиатором (E) =

= (De). Направление главных осей деформаций определяется углом

и для него, согласно (1.113), имеем:

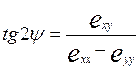      (1.117)

Главные удлинения

 

определяются формулами, аналогичными (1.116):

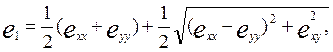
(1.118)

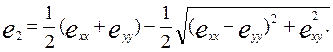
Октаэдрический сдвиг, согласно (1.51), равен:

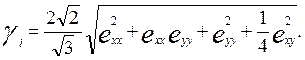             (1.119)

Направляющий тензор деформации (), кроме угла , определяется только одним числом  (1.80):

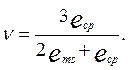                (1.120)

Можно себе представить два основных типа опытов с трубами.

Первый осуществляется на машинах, в которых по произволу экспериментатора могут быть заданы сила Р, давление р и крутящий мо- момент М. В таком случае, постепенно увеличивая определённым образом эти величины, можно измерять возникающие в трубе деформации, а именно: её осевое удлинение

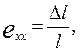
изменение диаметра

       

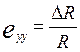
и угол закручивания  на длине :

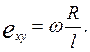
Затем, обрабатывая результаты по формулам (1.113), (1.111), (1.115),

(1.117), (1.119) и (1.120), можно искать зависимость между напряжениями и деформациями. Направляющие тензоры напряжений и де- деформаций будут равны между собой, если  и для любой комбинации внешних сил Р, р, М.

Второй тип опытов может быть осуществлён на машинах, позволяющих произвольным образом менять деформации трубы, а именно: её осевое удлинение, радиальное удлинение R и угол закручивания . Тогда приборы должны регистрировать возникающую силу Р, давление р и крутящий момент М. Обработка результатов останется прежней. Можно представить себе и опыты комбинированного типа.

Обычно делались опыты первого типа и притом частного характера.

Например, труба подвергалась действию только внутреннего давления и осевой силы. В таком случае из условий симметрии ясно, что кручение не возникает:

  

и потому совпадение главных осей обеспечивается автомати- автоматически. Таким образом, опыты без кручения позволяют найти связь между величинами и  В других случаях применялось только растяжение и кручение. Они позволяли найти связь между  и

а также между и .

Диапазон изменения угла и параметра, исчерпывающий все возможные случаи при плоском напряжённом состоянии, таков:

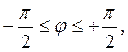
    (1.121)

В самом деле: 1) в случае равномерного растяжения в двух направлениях, когда

     , имеем

  

 и потом 2) в случае растяжения в одном направлении, когда

   

И потом   3) в случае сдвига, когда

    , и потому = — 1. Совпадение значений. в первом и четвёртом, а также во втором и пятом случаях очевидно, так как они отличаются только на величину равномерного всестороннего давления и растяжения (добавляя, например, в первом случае равномерное давление со всех сторон, равное, получим четвёртый случай и т. д.).

Если ещё принять во внимание, что механические свойства рассматриваемых металлов при растяжении и сжатии одинаковы, можно ограничить диапазон изменения величин и  значениями:

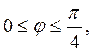
    (1.122)

Все имеющиеся опыты при сложном напряжённом состоянии с точки зрения излагаемой теории пластичности следует разбить на две  группы. К первой группе будем относить опыты, в которых осуществлялось простое нагружение трубы, т. е. для каждой данной трубы проводилось только одно испытание, в котором соотношение между прилагаемыми силами оставалось постоянным всё время, т. е. было постоянно и отношение главных напряжений . Так как направление главных осей напряжений при этом не могло изменяться относительно тела, то из простых условий симметрии ясно, что главные оси деформаций совпадали е главными осями напряжений. При этом совершенно несущественно — упрочняется ли в процессе деформации материал или не упрочняется. Итак, в случае простого нагружения условие:

выполняется автоматически. Вполне очевидно, что выполняется и условие=  во всех пяти перечисленных выше частных случаях, если нагружение являлось простым. В самом деле: 1) при равномерном растяжении в двух направлениях из условий симметрии ясно, что

     

и потому из (1.120) l; 2) в случае растяжения в одном направлении

  

и потому — 1; 3) в случае чистого сдвига утолщение или утоньшение стенки не происходит, и потому 0, т. е. = 0;

4) при простом сжатии в одном направлении

  

и потому l; 5) при равномерном двустороннем сжатии . Таким образом, в опытах при простой деформации условие  подлежит проверке только для , не равных 1,0 и — 1. Все эти значения могут быть достигнуты при испытании труб без кручения, и потому опыты на совместное действие растяжения и внутреннего давления при простом нагружении являются исчерпывающими. В самом деле, полагая

   

мы имеем из (1.115):

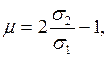
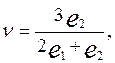                                    (1.123)

и потому при простом растяжении (р = 0, =0) имеем =—1;

при условии, т. е. при имеем. = 0 и, наконец, при равномерном двустороннем растяжении, т. е. при или при  имеем =1.

Опыты с простым нагружением математически можно определить условием, что в каждом отдельном испытании направляющий тензор напряжений остаётся неизменным, т. е. что все внешние силы (поскольку напряжённое состояние является однородным) в каждом испытании возрастают, пропорционально одному параметру:

     

причём величины   меняются только при переходе от одного испытания к другому. При этом и все напряжения оказываются пропорциональными , в том числе и октаэдрическое напряжение ибо будет функцией только  . Отметим следующее свойство таких опытов: если при всех значениях   . , а октаэдрическое напряжение есть функция только октаэдрической деформации т. е.:

то зависимости от и от отличаются между собой и от только масштабом, характерным для каждого опыта. В самом деле, из (1.123) и при имеем:

   

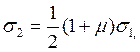
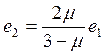
а потому, согласно (1.111) и (1.119), получаем:

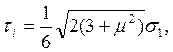
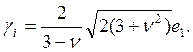     (1.125)

Так как отличаются от только масштабом, то указанное свойство становится очевидным.

Если материал трубы в результате деформации при одном испытании получает упрочнение, т. е. становится анизотропным, как это следует из эффекта Баушингера, второе испытание трубы при новом значении, вообще говоря, будет находиться в противоречии с первым. Поэтому, если необходимо проводить весь цикл испытаний

с одной и той же трубой, то её каждый раз следует путём термообработки приводить в одинаковое начальное состояние. Только тогда результаты различных испытаний будут сопоставимы.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Кафедра «Теоретической и прикладной механики»

                            Доклад

по «теории пластичности и ползучисти.»

                                                     Выполнил: студент Фоменко Е.А.

                                                       Группа 4ДМ-1

                                  Проверил: Олейников А.И.

Комсомольск - на - Амуре

2007