положение каждого из которых по отдельности при плоском движении характеризуется тремя параметрами, наложено четыре связи, одна из которых - дифференциальная интегрируемая. Следовательно, рассматриваемая механическая система является голономной с двумя степенями свободы:
s= 3N – k – g= 3ּ2 – 3 – l = 2,
где k- число геометрических связей; g-число дифференциальных связей.
В качестве обобщенных координат выберем горизонтальное смещение и центра масс диска и угол φповорота стержня – рисунок 3:
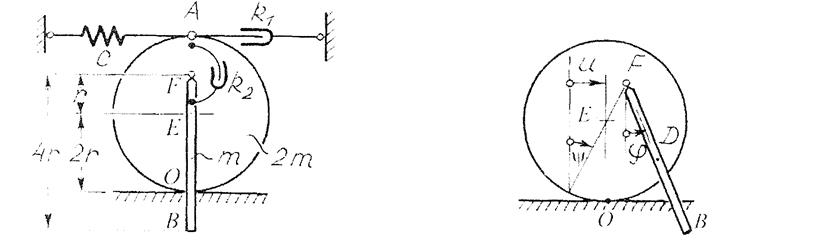
|
|
||||
Координаты любой точки механической системы, могут быть выражены через обобщённые. Покажем, как на основании уравнений связи (2), (4), (5), координаты из набора (1) выражаются через обобщенные:
![]() ,
, ![]() ,
, 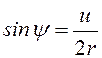 ,
,
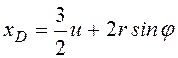 ,
, 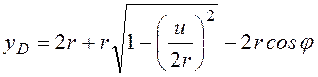 . (6)
. (6)
1.2 Дифференциальные уравнения малых колебаний
Дифференциальные уравнения малых колебаний получаем, используя уравнения Лагранжа второго рода в следующей форме:
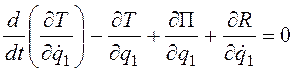 , i =
1, 2.
, i =
1, 2.
Здесь Т - кинетическая энергия, П - потенциальная энергия, R - диссипативная функция Рэлея.
Для вычисления Т, П и Rпридаем обобщенным координатам и обобщенным скоростям малые положительные значения (положительные значения и и φ показаны на рис. 5.3).
При вычислении кинетической энергии механической системы учитываем, что оба инерционных элемента совершают плоское движение:
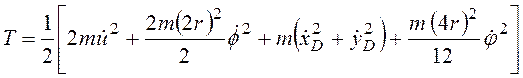 . (7)
. (7)
Потенциальная энергия механической системы складывается из потенциальной энергии деформации упругого элемента и потенциальной энергии положения центра тяжести физического маятника:
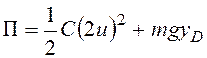 .
.
Примем допущение о малости отклонений механической системы от положения равновесия. В этом случае соотношения (6), связывающие физические координаты с обобщёнными координатами, могут быть упрощены:
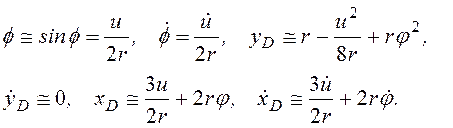 . (8)
. (8)
После подстановки выражений (8) в кинетическую и потенциальную энергии и учитывая заданное соотношение mg= Cr, получаем:
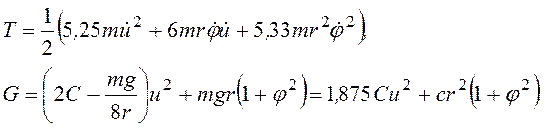 (9)
(9)
Диссипативная функция Рэлея, по определению равная половине мощности рассеяния энергии в демпферах, содержит два слагаемых, соответствующих демпферам k1и k2:
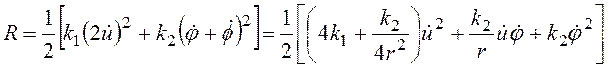 . (10)
. (10)
Подставляя Т, П, Rв уравнения Лагранжа второго рода, получаем:
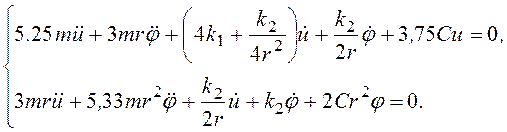 (11)
(11)
или в матричной форме
![]() .
.
Здесь {q} = ![]() - вектор-столбец обобщенных координат,
- вектор-столбец обобщенных координат,
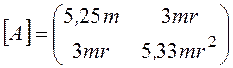 - матрица инерции,
- матрица инерции,
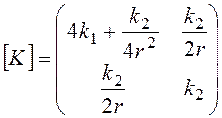 - матрица демпфирования,
- матрица демпфирования,
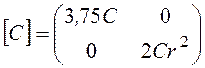 - квазиупругая матрица.
- квазиупругая матрица.
2 Собственные частоты и собственные формы механической системы
Строго говоря, собственные частоты диссипативной системы, описываемой уравнениями (11), это комплексные числа, определяющие как частоту колебаний системы, так и скорость их затухания. Точно так же формы колебаний представляются комплексными числами, показывающими, что эти формы характеризуются не только соотношением амплитуд масс системы, но и сдвигом фаз этих амплитуд друг относительно друга. Однако в подавляющем большинстве случаев, представляющих практический интерес, влияние трения как на собственные частоты колебаний, так и на их формы оказывается достаточно малым. Поэтому, под собственными частотами и формами диссипативной системы (11) понимают, обычно, собственные частоты и формы соответствующей консервативной системы, т.е. системы (12), получаемой из (11) отбрасыванием диссипативных членов:
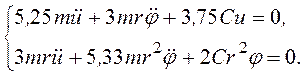 (12)
(12)
Решение системы (12) ищем в виде
u(t) = ucos(pt + α), (φ(t) – φcos(pt + α). (13)
Подставляя (13) в (12), получаем систему алгебраических уравнений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.