Задачи Аналитическая динамика:( Пятницкий Е.С.)
12.8 В следующих задачах движение системы определяется лагранжианом L. Найти движение системы, если
а) 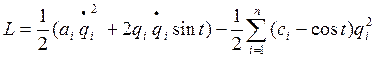
![]()
б) 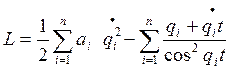
![]()
в) 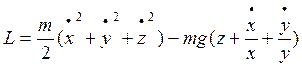
12.9. Свободная материальная
точка массы т движется в потенциальном силовом поле, причем П =П(x,у,z,t). Декартовы координаты точки х, у, zсвязаны с ортогональными криволинейными
координатами ![]() равенствами
равенствами
х = х(![]() ), У = У(
), У = У(![]() ), z = z(
), z = z(![]() ).
).
Найти лагранжиан точки в
координатах ![]() , используя коэффициенты Ламе
, используя коэффициенты Ламе
![]() =
= ![]()
![]()
( k=1,2,3)
12.10. Точка массы т движется в силовом поле с потенциалом П(x, у, z). Найти лагранжиан точки и составить ее уравнения движения в следующих системах координат:
а) цилиндрические координаты;
б) сферические координаты;
в) параболические координаты и,v, ![]() : х =
: х = ![]() у=
у=![]()
![]() .
.
12.11. Для плоского движения материальной точки
в силовом поле с потенциалом П (х, у) найти лагранжиан в координатах![]() и
и ![]()
![]() , связанных с декартовыми
координатами равенствами
, связанных с декартовыми
координатами равенствами
![]()
![]()
12.12. Найти функцию Лагранжа и составить
уравнения движения двух материальных точек с массами ![]() и
и
![]() , притягивающихся одна к другой по закону
Ньютона. Выписать также интегралы движения системы.
, притягивающихся одна к другой по закону
Ньютона. Выписать также интегралы движения системы.
Указание. За обобщенные координаты принять декартовы
координаты х, у, zцентра
масс системы, расстояние между точками rи углы ![]() и
и ![]() (широты
и долготы), которые определяют направление прямой, соединяющей точки.
(широты
и долготы), которые определяют направление прямой, соединяющей точки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.