Запись уравнения движения одной из консервативных систем в положении равновесия, пользуясь принципом Даламбера

число геометрических связей, наложенных на механическую систему;

g = 0 - число дифференциальных связей, наложенных на механическую систему.

Ограничения на абсолютные или взаимные положения либо скорости в рассматриваемой механической системе сводятся к запрещению перемещений точки О оси цилиндрического шарнира по двум взаимно перпендикулярным направлениям. Таким образом, геометрических связей две (d = 2), а дифференциальные связи отсутствуют (g= 0). Рассматриваемая механическая система является голономной и имеет одну степень свободы

n = 1.

Для голономной системы число обобщенных координат, однозначно определяющих положение механической системы, равно числу степеней свободы. В качестве обобщенной координаты примем угол поворота φ инерционного элемента 1 (см. рис. 1.2), отсчитываемый от положения статического равновесия,

q = φ.

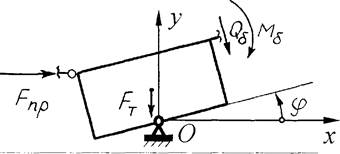
Рисунок 1.3 - Усилия, действующие на инерционный элемент

при его малом положительном отклонении

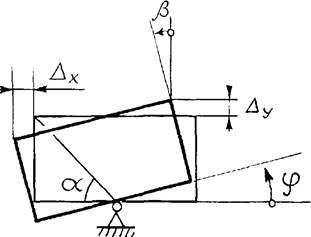
Рисунок 1.4 - Обозначения перемещений при малом положительном

отклонении инерционного элемента

2  Условие динамического равновесия

Поскольку рассматриваемое твердое тело имеет неподвижную ось вращения (ось z), то необходимым и достаточным условием его равновесия является следующее условие, связывающее активные силы:

= 0.                                                                (1.1)

Согласно принципу Даламбера любая система сил, приложенных к твердому телу, удовлетворяет условиям равновесия, если к этим силам добавить силы инерции. С учетом моментов сил инерции условие динамического равновесия рассматривае­мого тела примет вид

 = 0.                                                               (1.2)

Здесь  и  - моменты относительно оси z, проходящей через точку О, активных сил и сил инерции соответственно.

3  Уравнение движения

Условие (1.2) динамического равновесия является, по существу, неявной формой записи дифференциального уравнения движения рассматриваемого тела. Чтобы перейти к явной форме, необходимо выразить входящие в него величины через обобщенную координату φ и ее производные. Для этого выведем механическую систему из положения статического равновесия, придав инерционному элементу некоторый положительный угол поворота φ и малую положительную скорость . Отбросим взаимодействующие с инерционным элементом 1 пружину 2, упругую балку 3 (см. рисунок 1.2) и заменим их действие силовыми факторами F_пр, Q_б, М_б (рисунок 1.3). Тогда условие (1.2) динамического равновесия будет иметь вид

M_z(F_np) + M_z(Q_б) + M_z(M_б) + M_z(F_T) +  = 0.                                                               (1.3)

Здесь в левой части стоят моменты относительно оси zсилы пружины, поперечной силы балки , изгибающего момента, силы тяжести и сил инерции соответственно.

Величину и направление сил F_np, Q_б, М_б  определим в предположении малости отклонения инерционного элемента от положения статического равновесия. Пружина 2 при повороте инерционного элемента I против часовой стрелки (рисунок 1.4) укорачивается на величину

.

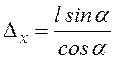Для б = р/4 получаем Δ_х =lφ. Такое деформирование упругого элемента приводит к возникновению в нем упругой силы:

                                                      F_np = CΔ_х = Clφ.

Момент этой силы относительно оси z:

M(F_np) = –F_npl(l – sin φ).                                                               (1.4)

Знак «–» в правой части поставлен потому, что сила F_npстремится повернуть элемент 1 по часовой стрелке, т.е. знак момента противоположен знаку угла φ.

Действующие со стороны упругой балки сила Q_би момент М_б обусловлены поворотом β и вертикальным отклонением Δ_у  сечения, соответствующего креплению балки 3 к инерционному элементу 1 (см. рисунок 1.2 и 1.3). Величины поперечной силы Q_би изгибающего момента М₆ в заделке, вызванные монтажными перемещениями β  и Δ_у, получим, используя расчетную схему один раз статически неопределимой балки (рисунок