Расчет положения равновесия системы. Исследование положения равновесия на устойчивость

Дано: G2 = 1,5G1    7c = 12G1

Требуется:

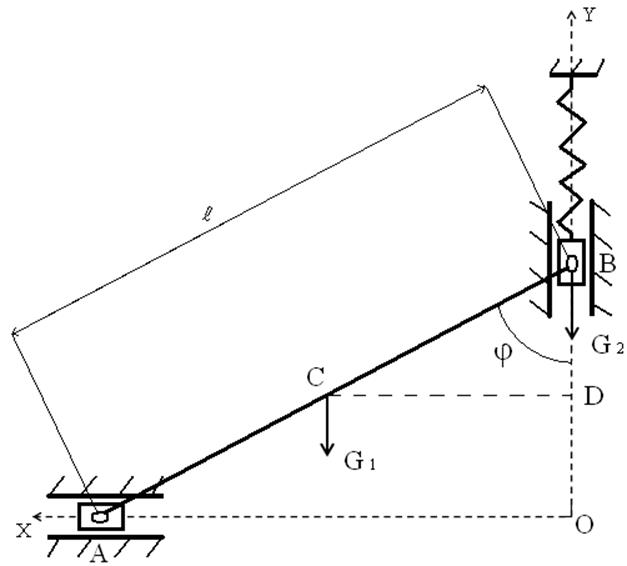
1) Найти положение равновесия системы.

2) Исследовать положения равновесия на устойчивость.

Решение:

G1 = 7c / 12;    G2 = 7c / 8

1) Определим положение равновесия системы. Для этого составим выражение потенциальной энергии, которая складывается из потенциальной энергии элементов системы в поле силы тяжести Пс.т и потенциальной энергии сил упругости деформированных пружин Пс.у

П = Пс.т + Пс.у

В качестве нулевого уровня потенциальной энергии элементов в поле сил выберем горизонтальную прямую, которая совпадает с осью горизонтальной симметрии нижнего ползуна.

 Тогда для каждого i–го элемента получим:

Пс.т(Gi)= Gi× yi

где Gi – вес i–го элемента, а yi – вертикальная координата центра тяжести i–го элемента. Тогда для нашей системы имеем:

Пс.т = G1 × y1 + G2 × y2

y2 =cosφ ×

Найдём y1, для этого рассмотрим подобные треугольники ABO и CBD в них:

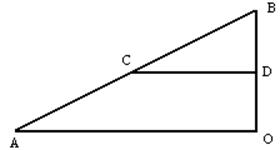
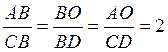 тогда BO = 2BD и значит BD = OD = ½ × OB

Отсюда:

y1 = y2 / 2

y1 = (cosφ × ) / 2

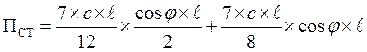
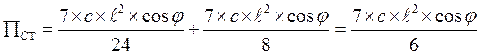
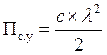    где   

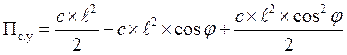
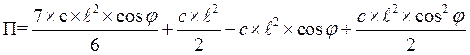
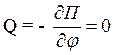
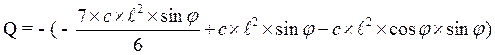
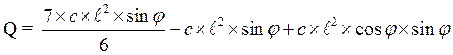
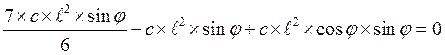
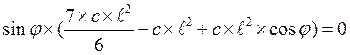
Получаем два уравнения:

   и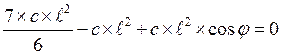   

Решая эти уравнения, получим:

;   ;      

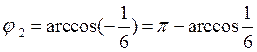2) Исследуем положения равновесия на устойчивость:

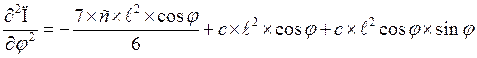
При φ = 0º

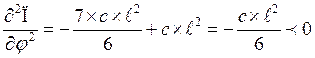     - положение равновесия не устойчивое.

При φ = 101º

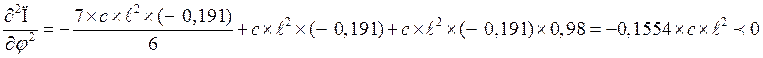
 - положение равновесия не устойчивое.