![]()
![]()
![]()
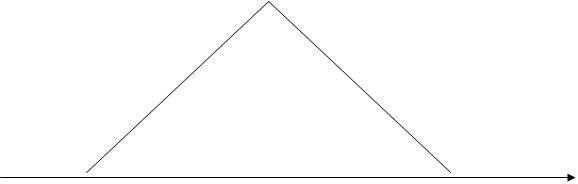 |
-T=-4,17 0 Т=4,17 t,мкс
2. По теореме Винера – Хинчина спектральная плотность мощности центрированного стационарного случайного процесса является преобразованием Фурье от корреляционной функции:
![]()
Используя теорему Винера-Хинчина найдем энергетический спектр стационарного процесса:
![]()
![]()
![]()
![]()
График спектральной
плотности средней мощности![]() модулирующего сигнала b(t)представлен
на рисунке.
модулирующего сигнала b(t)представлен
на рисунке.
![]()
![]()
![]()
![]()
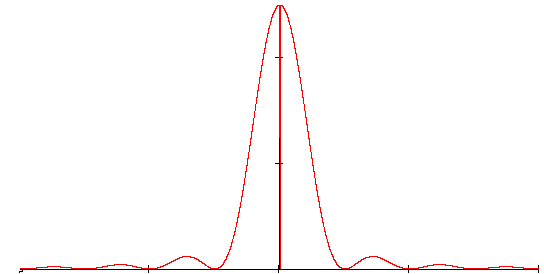
![]() -4/T
-3/T -2/T -1/T 0 1/T
2/T 3/T 4/T f,Гц
-4/T
-3/T -2/T -1/T 0 1/T
2/T 3/T 4/T f,Гц
Ширина спектра
Ограничим
сверху ширину спектра модулирующего сигнала частотой ![]() =
=![]()
Определим практическую ширину спектра модулирующего сигнала по первому нулю его огибающей:
Из графика огибающей видно, что ширина спектра по первому нулю будет равна 2/T.
Следовательно,
![]()
![]() .
.
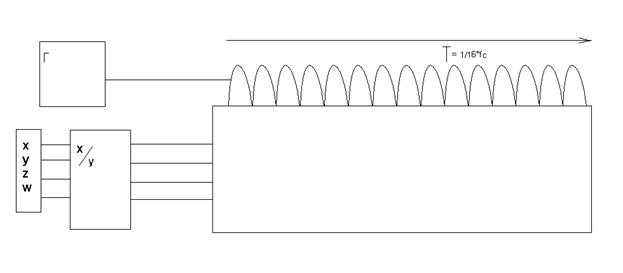
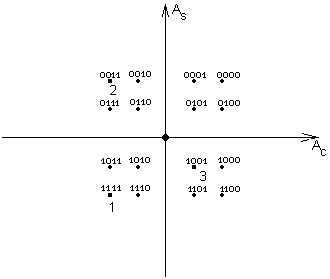
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.