Производительность труда, страница 4

t= (x - ) / σ

m¹=, где i – это величина интервала.

X²_факт = Σ 

X²_факт=(4-1,93)² /1,93 + (6-6,87)² /6,87  + (7-12,62)² /12,62 + (19-12,22)² /12,22 + (4-6,24)² /6,24 + (2-1,68)/1,68 = 9,45

X²_т = (p ; k) , где

      P=0,9935

k=n-r-1=6-2-1=3

Смотрим по специальной таблице значение X²_т=(0,9935 ; 3) = 13,28

Вывод: сравнивая фактическое и теоретическое значения, видим, что теоретическое больше фактического, следовательно, теоретическое распределение  подчиняется закону нормального распределения.

Критерий Колмогорова:

Для начала составим таблицу, где S_m это сумма эмпирических накопленных частот, S’_m это сумма теоретических накопленных частот. 

Sm	S’m	Sm-S’m
4	1,93	2,07
10	8,8	1,2
17	21,42	-4,42
36	33,64	2,36
40	39,88	0,12
42	41,56	0,44

λ = Д / √n

Д= max{ S_m-S’_m }=2,36

n = ∑m = 42

λ = 2,36/√42 = 2,36/6,48 = 0,364

По специальной таблице смотрим, какое значение p соответствует λ=0,364

Следовательно, p=0,997.

Вывод: С  вероятностью 0,997 можно утверждать, что отклонение в частотах является несущественным, а фактическое распределение подчиняется законам нормального распределения.

Задание №2

Определить ошибки выборки по результатам предыдущей задачи (типический способ отбора) и определить необходимый объем выборки при заданной β.

P=0.9935

β=1.2%

∆=t*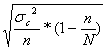, где

N=243

 n=93

t- коэффициент доверия, который определяется по специальной таблице, в зависимости от заданной вероятности.

t = 2.7

σ²=34

∆=2,7*√((34/93)*(1-93/243) ) = 2.7*√(0.3656*(1-0,3827)) = 1.28

Далее найдём среднюю генеральную совокупность

ˉx= x̃ ± Δ

 x̃= ∑x_i*m_i/∑m_i = (1250+1562,5) / (42+51) = 30,24

ˉx= 30,24 ± 1.28

Доверительный интервал:

28,96 ≤ ˉx ≤ 31,52

 β= Δ/x̃ *100%

 β= 1,28 / 30,24 *100% = 4,23%

Вывод: При объёме выборки в размере 93 человека из 243 и заданной вероятности относительная ошибка выборки составляет 4,23%, из чего следует что объём выборки достаточно высок, так как β менее 12%.

Далее определим объём выборки, так чтобы, относительная ошибка выборки β была равна 1,2%

Для начала найдём абсолютную ошибку выборки

Δ= (x̃*β) /100

Δ= (30,24*1,2) /100 = 0,362