Обзор наиболее часто применяемых параметрических критериев. 37
Общий обзор непараметрических критериев. 37
К теме 8. Выявление различий в уровне исследуемого признака.. 39
Параметрический критерий Стьюдента. 39
Непараметрический критерий Манна-Уитни. 41
К теме 9. Оценка достоверности сдвига в значениях исследуемого признака.. 43
Непараметрический критерий Вилкоксона. 43
К теме 10. Выявление различий в распределении признака.. 44
Критерий Колмогорова-Смирнова l. 44
К теме 11. Многофункциональные статистические критерии.. 47
Критерий φ* — угловое преобразование Фишера. 47
К теме 12. Дисперсионный анализ. 49
Введение в дисперсионный анализ ANOVA.. 49
Однофакторный дисперсионный анализ. 49
К теме 13. Многомерные методы обработки данных.. 53
Множественный регрессионный анализ. 53
Дискриминантный анализ («классификация с обучением») 54
Кластерный анализ («классификация без обучения») 54
Факторный анализ. 54
Многомерное шкалирование. 54
Глоссарий.. 55
Почти любая наука в процессе своего развития приходит к измерениям. Измерение можно рассматривать как построение своеобразной функциональной зависимости, в которой аргументами являются реальные величины (измеряемые объекты), а функциями — обозначающие их числа, меры. Причем функции должны обладать одним свойством — аддитивностью, то есть любые сложные преобразования реальных величин должны однозначно соответствовать операциям с их мерами (числами) и наоборот. Следовательно, 1) для измерения не обязательно нужно знать абсолютное значение величин, достаточно уметь определять их относительное изменение; 2) изучаемые явления вообще могут не характеризоваться определенными реальными величинами, их отношения и изменения должны носить определенный и сопоставимый характер — и они могут быть измерены; 3) измерение можно производить разнообразными способами; единственное условие, которое необходимо строго соблюдать — аддитивность принятой функции меры в соответствии с правилами измерения.
Измерение — приписывание числовых форм объектам или событиям в соответствии с определенными правилами (Стивенс, 1960 г.).
На рисунке 1 приведена схема, в которой отражены типы измерений, методы, которыми они выполняются, и измерительные шкалы, получаемые при использовании этих методов.
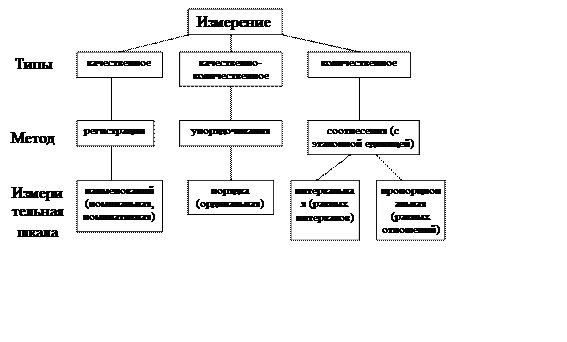
Рис.1. Типы измерений и измерительные шкалы
При измерении методом регистрации правила измерения таковы, что они позволяют лишь установить, что один объект отличается по измеряемому свойству от другого объекта, у которого измеряемое свойство качественно иное. Поэтому в результате объекты классифицируются по группам (классам), которые могут быть обозначены номерами, названиями, именами и т.п. Обозначение класса не измеряется количественно, оно лишь позволяет отличить один объект от другого в отношении измеряемого свойства. Это и составляет сущность шкалы наименований (синонимы — номинальная шкала, номинативная шкала).
Безразлично, в каком порядке будут расположены классификационные ячейки (названия групп). То, что номер одного класса больше или меньше другого, ещё ничего не говорит о свойствах объектов, за исключением того, что они различаются.
Единицей измерения, которой мы оперируем, является количество объектов, принадлежащих данному классу, (испытуемых, реакций людей, выборов и т.п.), или частота (абсолютная частота), относительная частота (частость, вероятность), процентная частота. С числами, получаемыми в результате измерения методом регистрации, нельзя производить арифметические операции.
Примеры шкалы наименований: пол, национальность, семейное положение, образование, здоровый – больной, клинические диагнозы, левша – правша, тип темперамента, тип личности и т.п.
При измерении методом упорядочивания правила измерения таковы, что мы уже можем сравнить объекты по принципу «больше — меньше измеряемого свойства
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.