








В соответствии с
условиями сходимости этот ряд сходится во всех точках кроме точки t = 0,
где он равен полусумме левого и правого пределов в этой точке  . Это действительно так, потому что
. Это действительно так, потому что ![]() .
.
6.5. Функции Бесселя
Бесселевыми или цилиндрическими функциями называются решения линейного дифференциального уравнения Бесселя
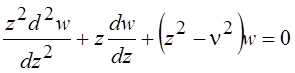 ,
(6.13)
,
(6.13)
где z – комплексная переменная, ν – параметр, порядок, значок или индекс, также может быть произвольным комплексным числом.
В приложениях часто
приходится рассматривать случай, когда ν = n – целое число. Под
цилиндрическими функциями понимают следующие функции: функции Бесселя Jν(z), функции Неймана Nν(z), часто называемые функциями
Вебера с обозначением Yν(z), и функции Ганкеля Hν(1)(z), Hν(2)(z). Названные функции при
фиксированном ![]() являются аналитическими функциями
z. Часто функции Бесселя приходится рассматривать при фиксированном z
как функции значка ν. При этом она является целой функцией комплексной переменной
ν.
являются аналитическими функциями
z. Часто функции Бесселя приходится рассматривать при фиксированном z
как функции значка ν. При этом она является целой функцией комплексной переменной
ν.
Целой функцией называется
аналитическая функция, представимая всюду сходящимся рядом Тейлора 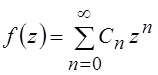 .
.
Между функциями Jν(z), Nν(z) или Yν(z), Hν(1)(z), Hν(2)(z) имеют место зависимости, аналогичные формулам Эйлера:
![]() ;
; ![]() .
.
С физической точки зрения гармонические функции описывают незатухающие колебания постоянной частоты, в то время как функции Бесселя характеризуют слабозатухающий осциллирующий процесс, частота которого становится постоянной лишь в ассимптотике.
Отыскивая решение
уравнения (6.13) в виде обобщённого степенного ряда 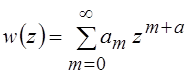 , где am и a – подлежащие определению
коэффициенты и значение параметра соответственно, получим два частных решения:
, где am и a – подлежащие определению
коэффициенты и значение параметра соответственно, получим два частных решения:
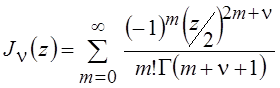 ;
; 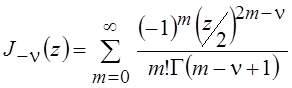 , (6.14)
, (6.14)
которые при ![]() являются
линейно независимыми и их линейная комбинация образует общее решение уравнения
(6.13).
являются
линейно независимыми и их линейная комбинация образует общее решение уравнения
(6.13).
Если ν = n, то
между функциями Jп(z) и J–п(z) существует линейная зависимость вида ![]() .
.
Для получения общего решения уравнения (6.13) для ν = n и вводится функция Неймана
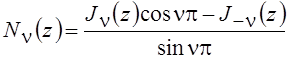 .
.
Функции Jν(z) и Nν(z) образуют фундаментальную линейно независимую систему решений уравнения Бесселя при любых значениях v, в том числе и при целых.
Функции Бесселя чисто мнимого аргумента (модифицированные функции Бесселя).
Если считать, что ![]() , где x – вещественная переменная,
то подставляя это значение в (6.14), получим:
, где x – вещественная переменная,
то подставляя это значение в (6.14), получим:
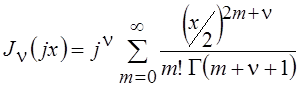 ;
; 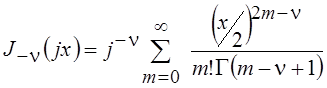 .
.
Входящие в эти выражения ряды и определяют модифицированные функции Бесселя
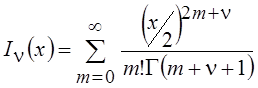 ;
; 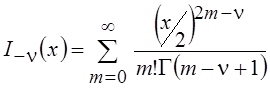 . (6.15)
. (6.15)
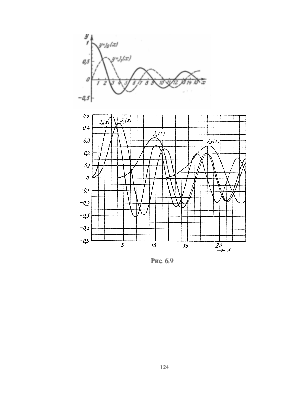
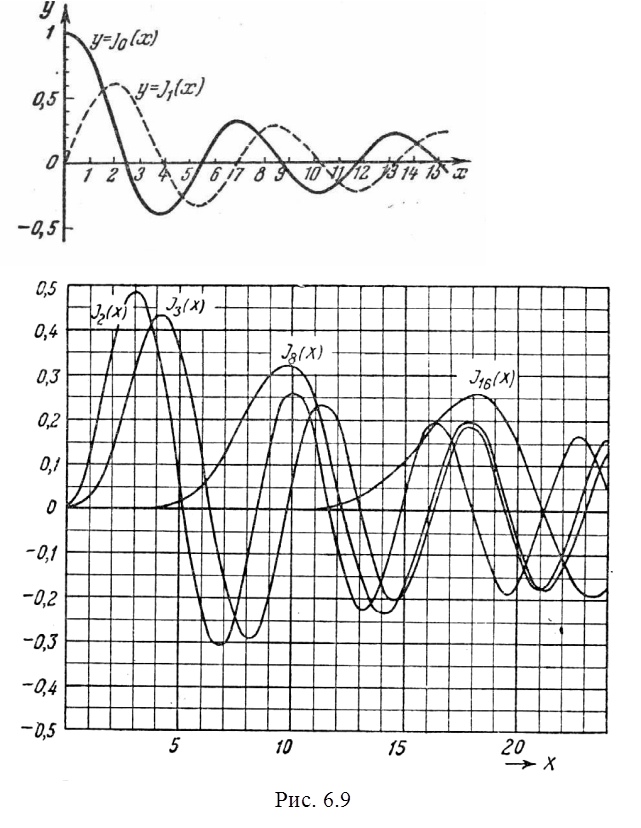
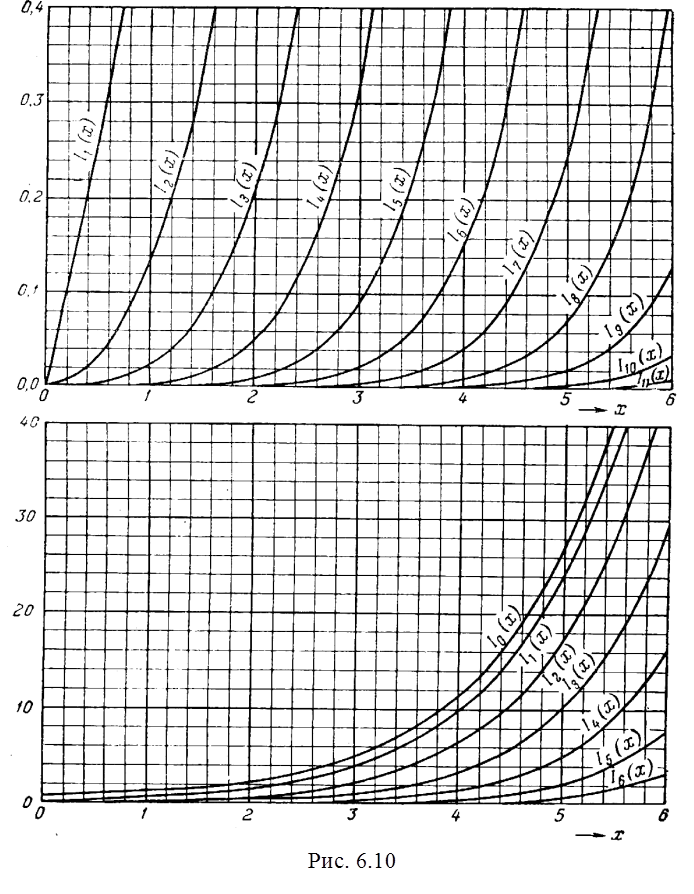
То, что ряды (6.14) являются знакопеременными, а (6.15) – знакопостоянными определяет резкое различие в их поведении (см. рис.6.9 и рис.6.10, на которых представлены графики функций Jn(x) и In(x) соответственно).
Далее будем считать аргумент функции Бесселя вещественным числом х. Правило дифференцирования функций Бесселя определяется следующим рекуррентным соотношением:
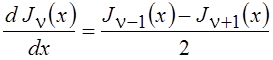 .
.
В частности, при ![]() с учётом того, что
с учётом того, что ![]() ,
получим:
,
получим:
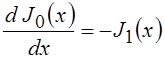 .
.
Три соседних по значку функций Бесселя связаны соотношением
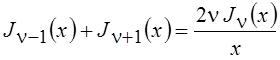 .
(6.16)
.
(6.16)
Аналогичные формулы имеют место и для модифицированных функций Бесселя:
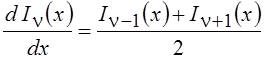 ;
; 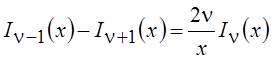 .
.
Из определения (6.15),
учитывая поведение гамма-функции при отрицательных целых значениях аргумента,
нетрудно показать, что I-n(x) = In(x) и, следовательно, 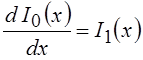 .
.
При полуцелом значке 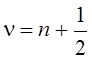 , где n – целое число, функции
Бесселя выражаются через элементарные функции, так как выполняются соотношения
, где n – целое число, функции
Бесселя выражаются через элементарные функции, так как выполняются соотношения 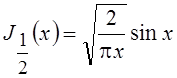 и
и 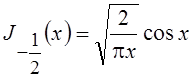 , что
позволяет с помощью рекуррентного соотношения (6.16) определить
, что
позволяет с помощью рекуррентного соотношения (6.16) определить 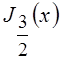 и так далее.
и так далее.
Общие выражения для
функций Бесселя полуцелого значка имеют вид 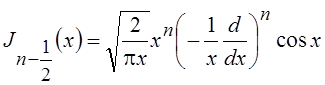 и
и 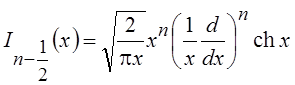 , где символ
, где символ 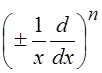 означает
п-кратное дифференцирование стоящего за ним выраже- ния с умножением результата
на
означает
п-кратное дифференцирование стоящего за ним выраже- ния с умножением результата
на ![]() после каждого дифференцирования.
после каждого дифференцирования.
Последующее дифференцирование проводится с учетом этого множителя. Например,
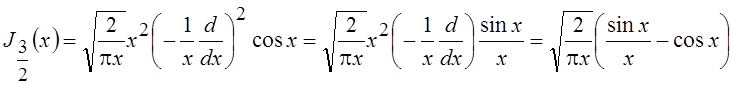 .
.
Приведенные выражения еще раз подчеркивают осциллирующий и слабозатухающий характер поведения функций Бесселя.
При изучении
асимптотического поведения функции Бесселя рассматривают разные сценарии
поведения аргумента z и значка v. Наиболее интересным и простым
является случай, когда v фиксировано, а ![]() . В этом
случае первое приближение для
. В этом
случае первое приближение для 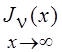 имеет вид
имеет вид 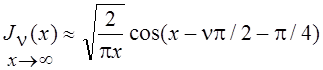 , и, соответственно,
, и, соответственно, 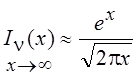 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.