Другие предметы \ Математический аппарат радиотехники

Функции Бесселя (Бесселевые или цилиндрические функции), страница 2

Важной особенностью функций Бесселя является увеличение с ростом v промежутка , на котором функция Бесселя близка к нулю.

Как и для других специальных функций, важную роль в их изучении играют производящие функции. Так, например, если разложить функцию 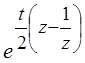 комплексной переменной z и вещественной t в ряд Лорана в окрестности существенно  особой точки z = 0, то получим

.

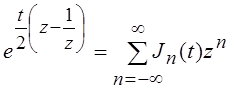Полагая и записывая условия равенства комплексных чисел, получим два важных для практики разложения:

,

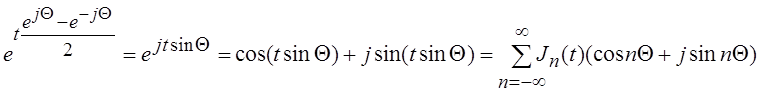откуда следует, что

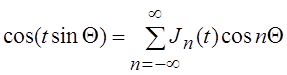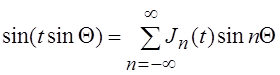; .         (6.17)

Пользуясь тем, что  и учитывая четность косинуса и нечетность синуса, эти выражения можно записать в виде

 ; .

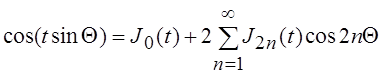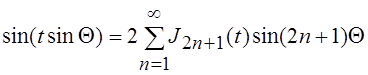Если заменить в этих выражениях   на , то получим

; .

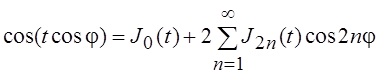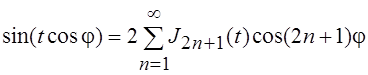Эти разложения носят имя Якоби, впервые их получившего.

Умножая левую и правую части первого равенства (6.17) на , а вторую на  и интегрируя от 0 до , получим:

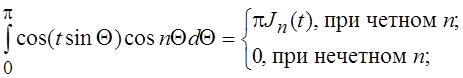
и

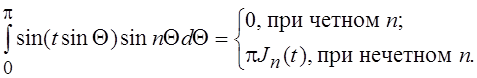
Складывая эти равенства, находим, что при любом п:

.

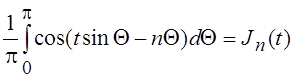Этот интеграл, который можно рассматривать как интегральное представление функции Бесселя с целым значком, называется интегралом Бесселя. При п = 0 интеграл Бесселя обращается в интеграл Парсеваля:

.

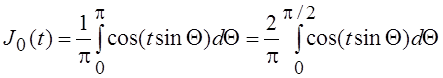Во многих задачах оказываются полезными теоремы сложения для бесселевых (цилиндрических) функций, простейшей из которых является следующая.

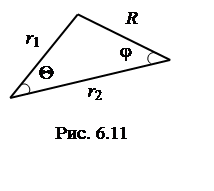Пусть  – стороны треугольника, приведенного на рис.6.11, а  и  – его углы, лежащие против сторон  и , так, что в соответствии с теоремами косинусов и синусов  и .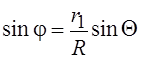

Тогда для  имеет место разложение вида

,

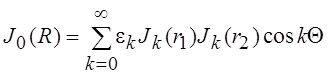называемое формулой Неймана, где 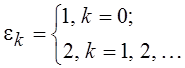 – символ Неймана. Поскольку при замене R ® lR, r1 ® lr1, r2 ® lr2  углы Q и j не изменятся, то приведенную выше формулу можно записать в следующем виде:

.

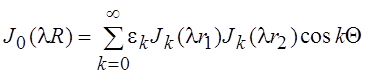При l = j с учетом того, что Jk(x) = j kIk(x), k = 0, 1, 2, …, получим:

.

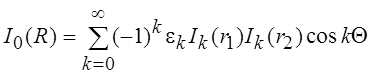Для произвольного значка v теоремы сложения для Jv(R) и Iv(R) примут вид:

,

.

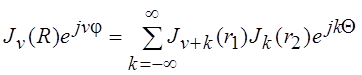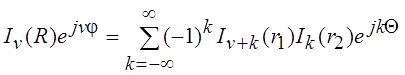Нули цилиндрических функций и разложение функций в ряды Фурье-Бесселя.

Как уже отмечалось выше, нули базовой или материнской функции определяют масштабный коэффициент при построении базисной системы на основе функций Бесселя. Рассмотрим уравнение . Корни этого уравнения называются нулями функции Бесселя  и обозначаются как

Нули функций Бесселя  и  перемежаются. Можно показать [14], что система функций 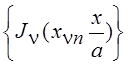, где  – n-й корень уравнения , ортогональна на промежутке  с весом x, т. е.

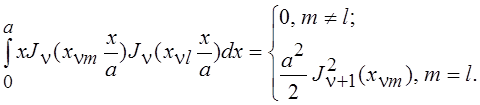
Так как нули соседних по индексу функций Бесселя перемежаются, то .

Если функция f(x) кусочно-непрерывна и обладает ограниченным изменением в любом интервале (c, d), удовлетворяющем условию 0 <  c< d < a, и существует интеграл 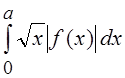, то ряд Фурье–Бесселя 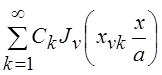, где 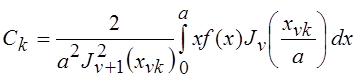, сходится и имеет сумму 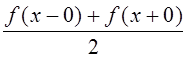, т. е. совпадает с f(x) в каждой точке ее непрерывности.

Приведем пример использования функций Бесселя в различных задачах.

Спектр частотномодулированного (ЧМ) колебания при гармоническом законе модуляции.

Найдем спектр сигнала, мгновенная частота которого равна , где  – девиация  частоты,  – несущая частота,  – частота модуляции. Так как фаза колебания , то в нашем случае 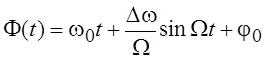 . Отношение  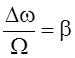называется индексом модуляции. Как мы увидим из дальнейшего, именно он определяет структуру спектра ЧМ колебания при гармоническом законе модуляции. Произвольную постоянную – начальную фазу  без потери общности можно положить равной нулю. Таким образом,  исследуемый сигнал имеет вид:

,

где  – амплитуда колебания.

Используя известную формулу , запишем наш сигнал в виде

.

Применяя разложения (6.17) и упомянутую выше тригонометрическую формулу, получим окончательное выражение для спектра ЧМ колебания при гармоническом законе модуляции:

.

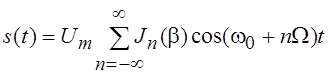Таким образом, спектр исследуемого сигнала имеет дискретный характер, причем амплитуды гармоник определяются номером n и индексом модуляции. Учитывая осциллирующий характер поведения функций Бесселя, отметим что при изменении индекса модуляции  меняются соотношения между амплитудами гармоник.

Обращаясь к рис. 6.9, нетрудно заметить, что при отличными от нуля будут лишь функции ,  и  , напомним что  и   отличаются только знаком. Таким образом, при

.

Если к этому добавить, что при   можно полагать  и 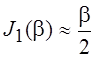, то окончательно получим:

Скачать файл