Структурный метод. Область применимости структурного метода

Определим модальные характеристики по характеристическому уравнению

Оно имеет два корня, которые в зависимости от коэффициента демпфирования могут быть вещественными и комплексно - сопряженными, что приводит к различным переходным процессам в звене.

Если , то звено второго порядка называют колебательным. Его переходная функция следующая:

Колебательность переходного процесса зависит от коэффициента демпфирования d: она будет тем больше, чем меньше d. При d = 0 имеют место незатухающие колебания.

Определим частотные характеристики звена, заменив p на j в передаточной функции (3.41).

Отсюда получим выражения для ВЧХ и МЧХ в виде:

При построении АФХ на комплексной плоскости необходимо рассматривать характерные точки:

На основе выражения

строится ЛАЧХ.

Асимптотическую ЛАЧХ колебательного звена (при ) также можно построить, если рассматривать отдельно области высоких и низких частот и для каждой определить свою асимптоту:

Частота называется собственной частотой колебательного звена. Причем на этой частоте для асимптотической ЛАЧХ справедливо соотношение: .

При с достаточной точностью можно применять асимптотическую ЛАЧХ звена.

произведения двух передаточных функций апериодических звеньев:

где - постоянные времени апериодических звеньев. В этом случае асимптотическая ЛАЧХ звена второго порядка имеет два излома на частотах . Она может быть получена суммированием асимптотических ЛАЧХ двух апериодических звеньев.

В начало

3.8.1. Последовательное соединение звеньев

Рассмотрим последовательное соединение типовых звеньев и найдем выражение для общей передаточной функции.

Рис. 3.26. Структурная схема последовательного соединения звеньев.

Утверждение: передаточная функция последовательного соединения звеньев равна произведению передаточных функций всех звеньев.

Для доказательства найдем выходную переменную системы

Отношение y к u дает передаточную функцию (3.52).

В начало

3.8.2. Параллельное соединение звеньев

Параллельное соединение звеньев изображено на рис.3.27.

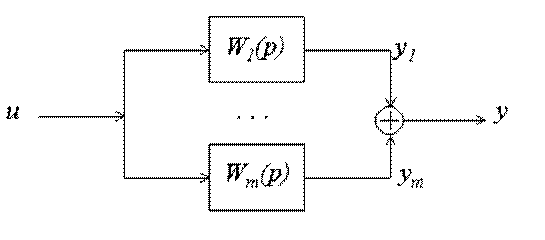
Рис.3.27 Структурная схема параллельного соединения звеньев

Утверждение: передаточная функция параллельного соединения звеньев равна сумме передаточных функций всех звеньев:

Доказательство аналогично п.3.8.1.

В начало

3.8.3. Обратная связь

Звено, охваченное обратной связью, приведено на рис.3.28.

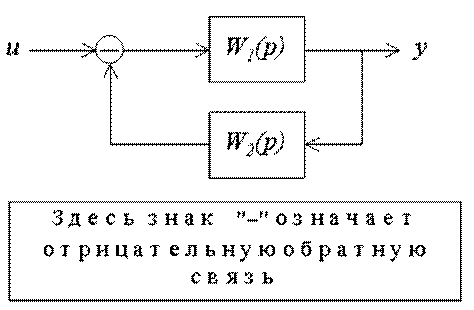
Рис.3.28. Структурная схема звена, охваченного обратной связью

Запишем выражение для выходной переменной

из которого можно найти передаточную функцию системы

Таким образом, передаточная функция системы с отрицательной обратной связью равна дроби, числитель которой соответствует передаточной функции прямого канала, а знаменатель есть сумма единицы и произведения передаточных функций прямого и обратного каналов.

В случае положительной обратной связи формула (3.54) принимает вид

На практике обычно встречаются системы с отрицательной обратной связью, для которых передаточная функция находится по соотношению (3.54).

3.8.4. Правило переноса

Иногда при структурных преобразованиях для получения общей передаточной функции системы удобнее переносить точку приложения сигнала через звено.

Рассмотрим, как изменится структура системы, если перенести точку приложения сигнала на выход.

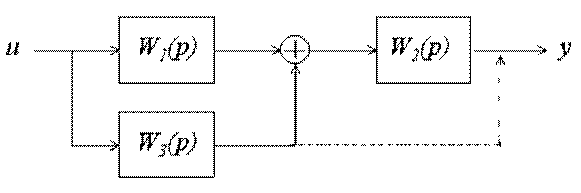
Рис.3.29. Структурная схема исходной системы

Ее передаточная функция имеет вид

При переносе точки приложения сигнала необходимо придерживаться правила: передаточная функция системы должна оставаться неизменной. Поэтому преобразованная система будет иметь вид:

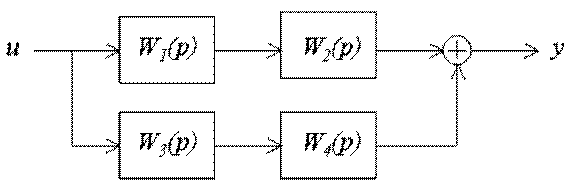
Рис.3.30. Структурная схема преобразованной системы

Передаточная функция системы, представленной на рис.3.30, следующая:

Приравнивая передаточную функцию (3.56) к функции (3.57), определим которую необходимо ввести в систему,

Того же правила следует придерживаться при обратном переносе точки отбора сигнала.

В начало

3.9. Переход от передаточных функций к уравнениям
состояния с использованием структурных схем

Рассмотрим одноканальную систему с известной передаточной функцией

которую можно представить в виде произведения двумя различными способами:

Эти два варианта представления передаточной функции системы приводят к двум различным формам уравнений состояния.

Рассмотрим переход к дифференциальным уравнениям от первого