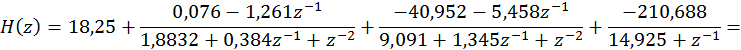
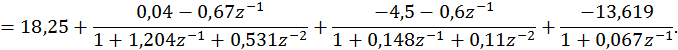
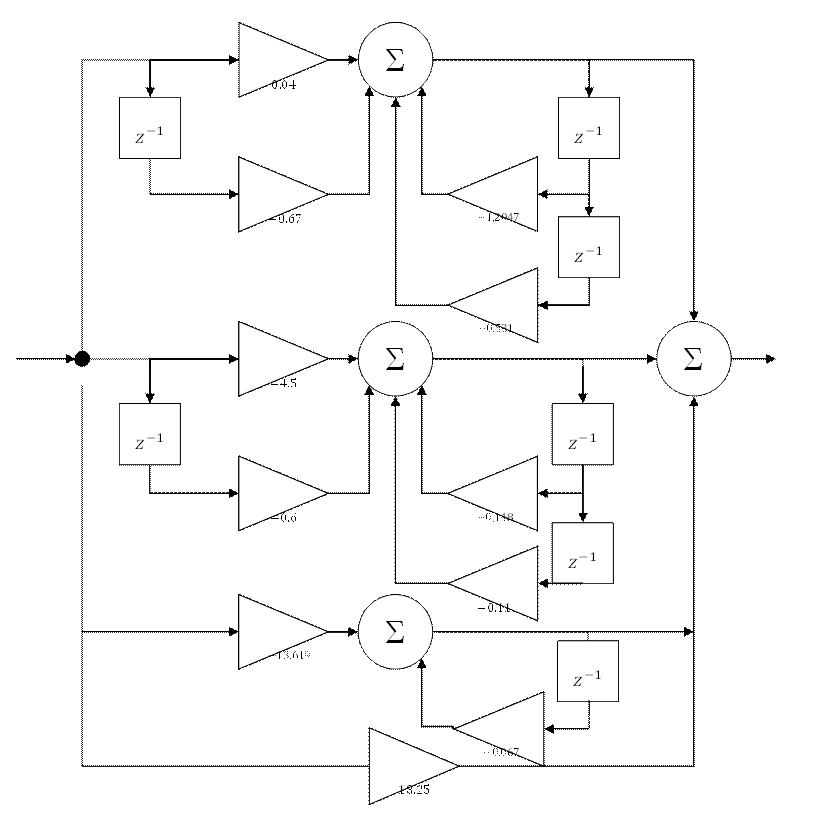
Рис.15 Параллельная форма реализации ДФ.
Реализация последовательной схемы ДФ производится при представлении исходной системной функции в виде произведения нескольких парциальных системных функций:
![]()
каждая из которых соответствует дискретному фильтру порядка не выше второго (порядок фильтра равен числу полюсов его системной функции). Тогда нашу системную функцию можно представить следующим образом:
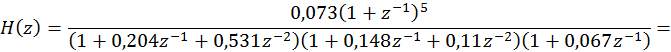
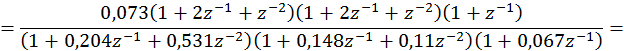
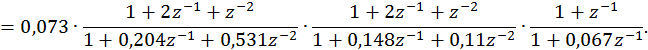
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()

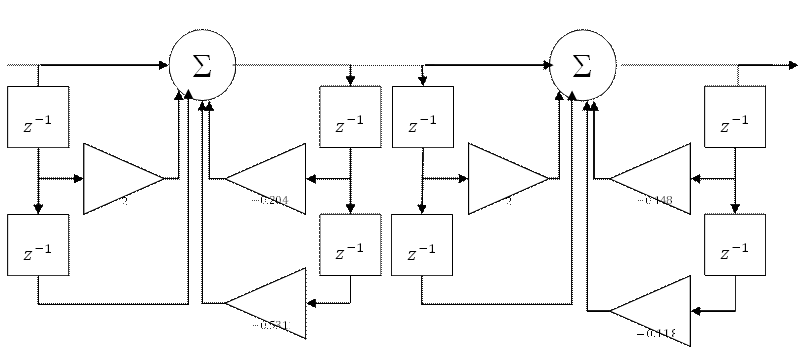
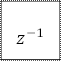
 |
Рис.16 Последовательная форма реализации ДФ.
Сигнал на выходе фильтра рассчитывается по следующей формуле:
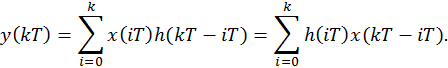
Тогда сигнал, изображённый на рисунке 7, при прохождении через фильтр имеет следующий вид
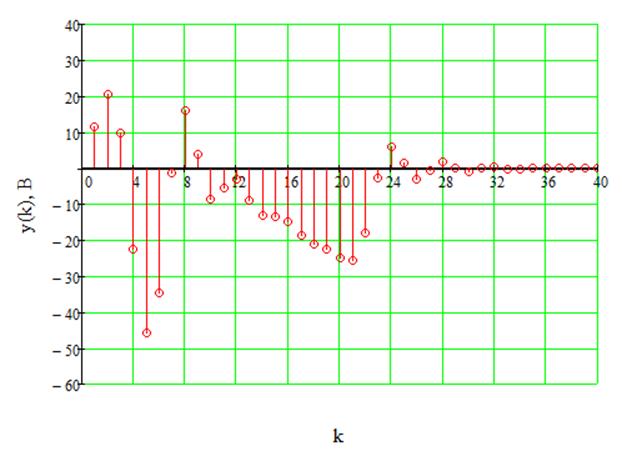
Рис.18. Исходный сигнал на выходе ДФ.
Дискретизированный входной сигнал в виде прямоугольного видеоимпульса и выходной сигнал дискретного фильтра изображены соответственно на рисунках 19 и 20. Расчёт выходного сигнала осуществляется по следующей формуле:
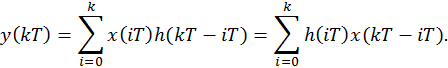
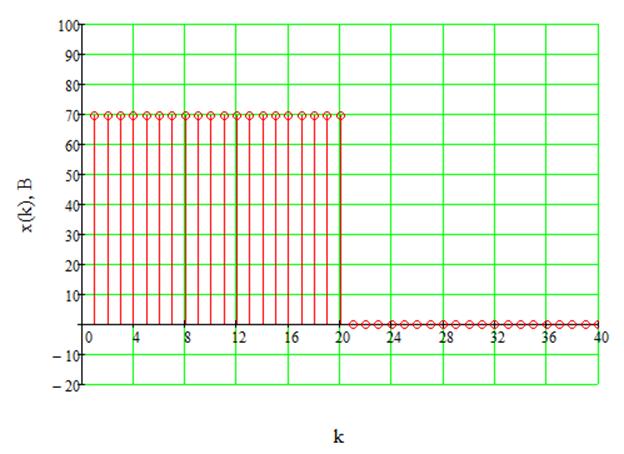
Рис.19. Дискретизированный прямоугольный видеоимпульс.
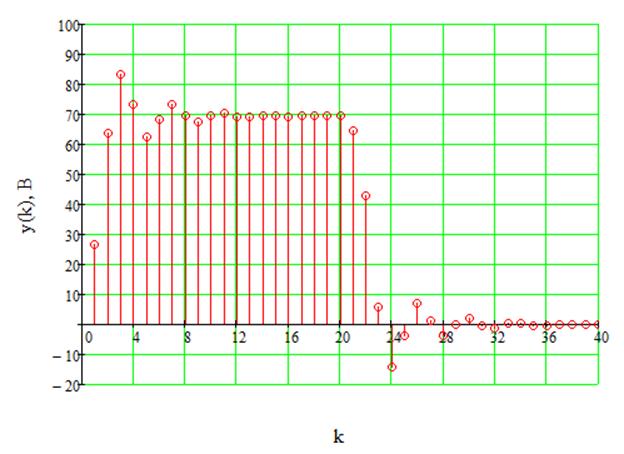
Рис.20. Прямоугольный видеоимпульс на выходе ДФ.
Дискретизированный входной сигнал в виде меандра и выходной сигнал дискретного фильтра изображены соответственно на рисунках 21 и 22. Расчёт выходного сигнала осуществляется по следующей формуле:
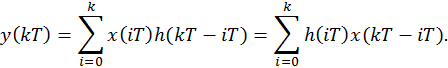
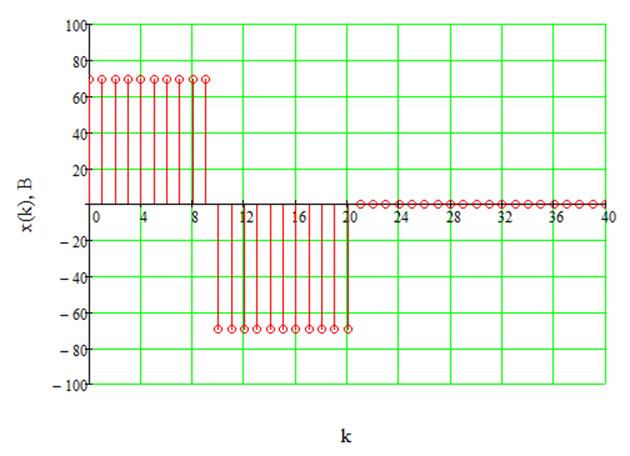
Рис.21. Дискретизированный меандр.
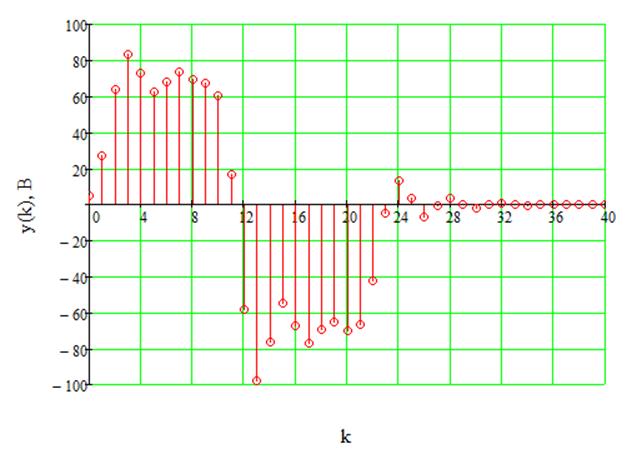
Рис.22. Меандр на выходе ДФ.
Дискретизированный входной сигнал в виде треугольного импульса и выходной сигнал дискретного фильтра изображены соответственно на рисунках 23 и 24. Расчёт выходного сигнала осуществляется по следующей формуле:
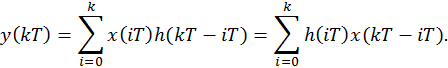
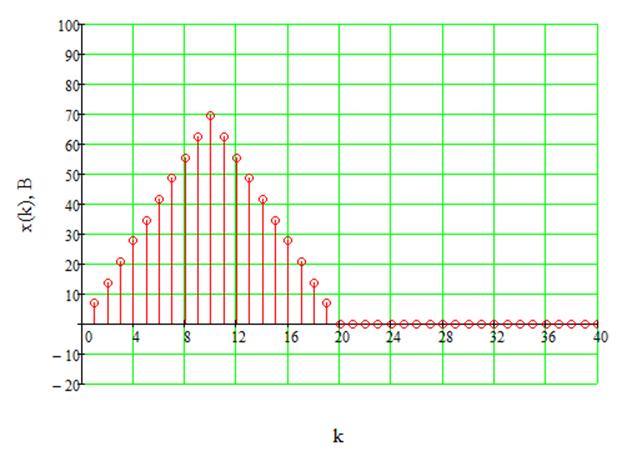
Рис.23. Дискретизированный треугольный импульс.
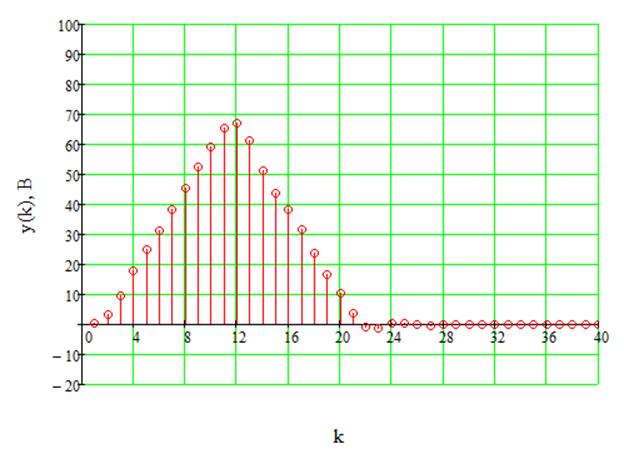
Рис.24. Треугольный импульс на выходе ДФ.
График входной реализации случайного процесса и график выходной реализации ДФ изображены на рисунках 25 и 26 соответственно.
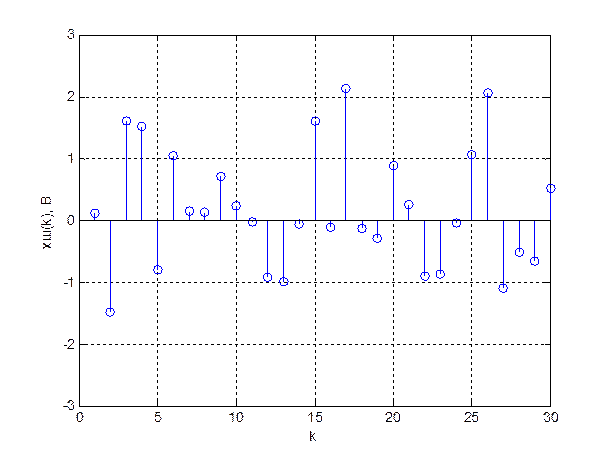
Рис.25. Входная реализация случайного процесса.
С
помощью программы определяем, что математическое ожидание процесса на входе ![]() , а СКО
, а СКО
![]() дисперсия
дисперсия
![]()
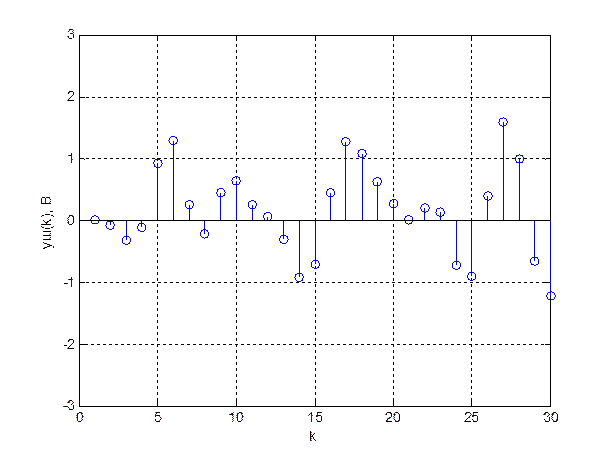
Рис.26. Реализация случайного процесса на выходе ДФ.
С
помощью программы определяем, что математическое ожидание процесса на выходе ![]() , СКО
, СКО ![]() , дисперсия
, дисперсия
![]()
Графики дискретных КФ входного и выходного шума изображены на рисунках 27 и 28 соответственно.
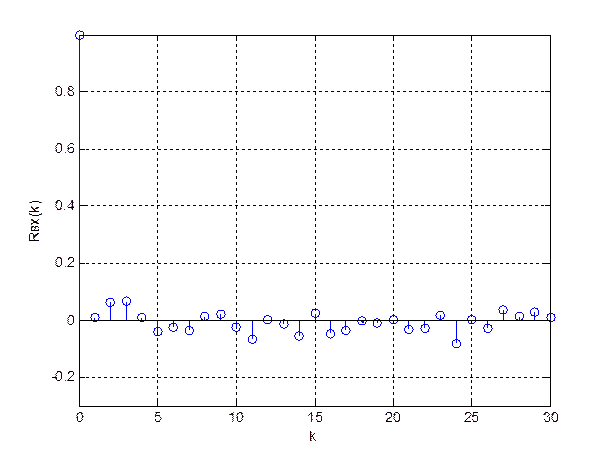
Рис.27. КФ входного шума.
Интервал корреляции рассчитывается по следующей формуле и равен
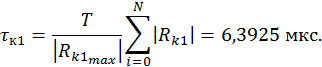
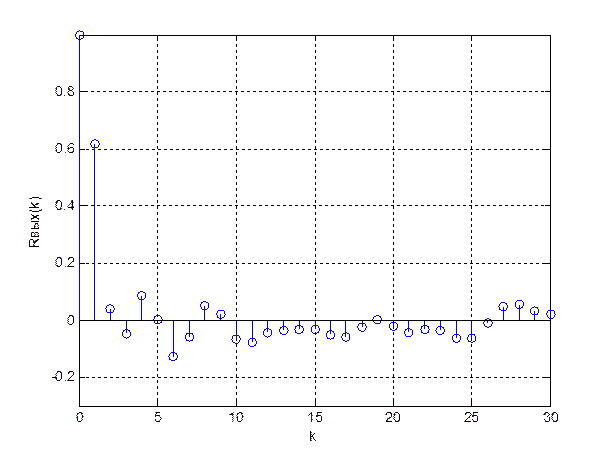
Рис.28. КФ выходного шума.
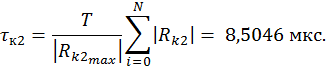
Отношение сигнал/шум на входе равно 3:1, т.е ![]() .
Аддитивная смесь сигнала и шума на входе и выходе ДФ показаны на рисунках 29 и
30 соответственно.
.
Аддитивная смесь сигнала и шума на входе и выходе ДФ показаны на рисунках 29 и
30 соответственно.
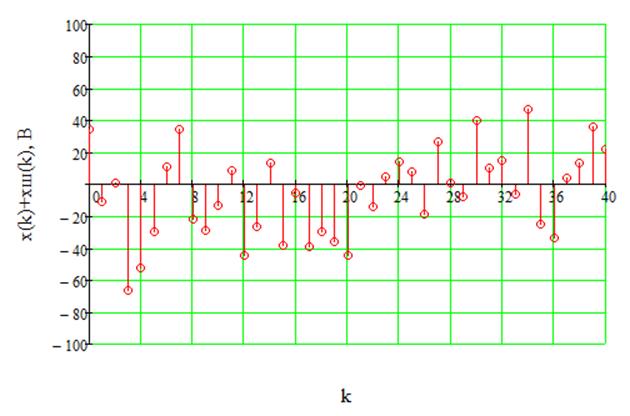
Рис.29. Аддитивная смесь сигнала и шума на входе ДФ.
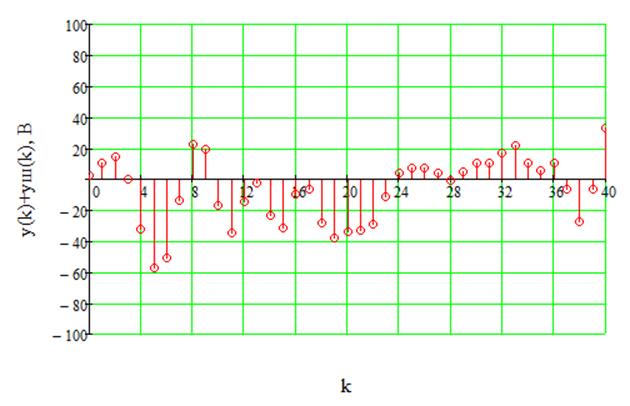
Рис.30 Аддитивная смесь сигнала и шума на выходе ДФ.
![]()
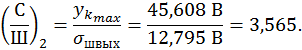
Отношение сигнал/шум на входе равно 1:1, т.е ![]() .
Аддитивная смесь сигнала и шума на входе и выходе ДФ показаны на рисунках 31 и
32 соответственно.
.
Аддитивная смесь сигнала и шума на входе и выходе ДФ показаны на рисунках 31 и
32 соответственно.
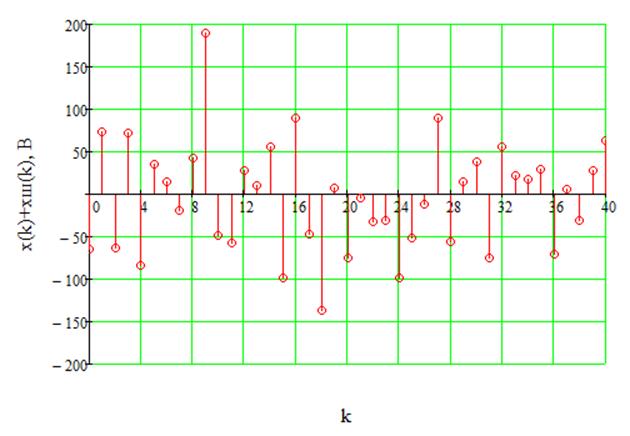
Рис.31. Аддитивная смесь сигнала и шума на входе ДФ.
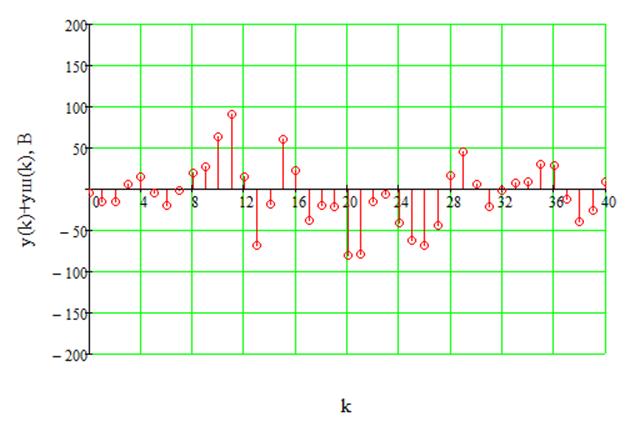
Рис.32. Аддитивная смесь сигнала и шума на выходе ДФ.
![]()
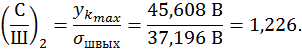
Отношение сигнал/шум на входе равно 1:2, т.е ![]() .
Аддитивная смесь сигнала и шума на входе и выходе ДФ показаны на рисунках 33 и
34 соответственно.
.
Аддитивная смесь сигнала и шума на входе и выходе ДФ показаны на рисунках 33 и
34 соответственно.
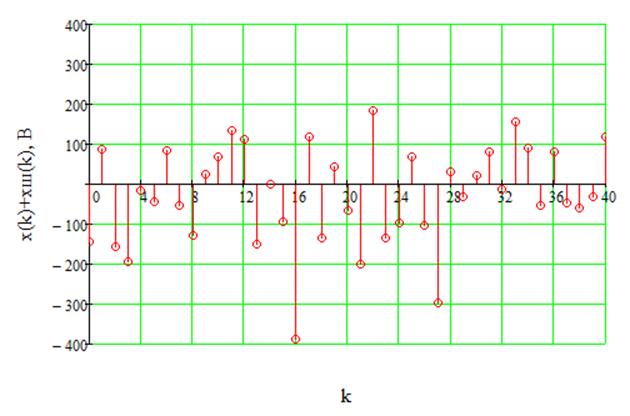
Рис.33. Аддитивная смесь сигнала и шума на входе ДФ.
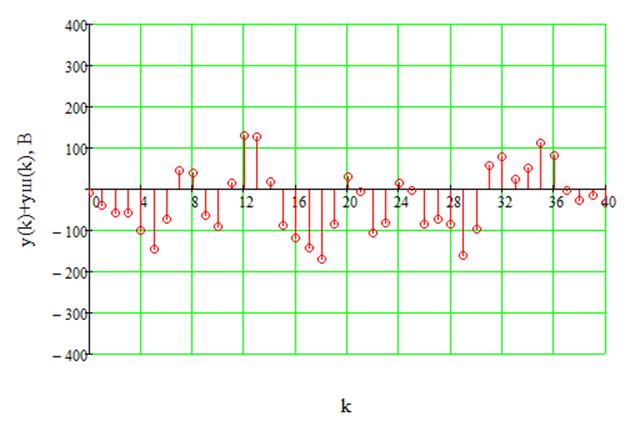
Рис.34 Аддитивная смесь сигнала и шума на выходе ДФ.
![]()
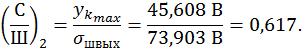
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.