Синтез и анализ дискретного фильтра, выполненного на основе аналогового фильтра Батерворта

Постановка задачи.

1. В качестве входного сигнала в курсовой работе рассматривается дискретизированный видеоимпульс , где  - интервал дискретизации.

Входной сигнал задается с вариацией параметра , принимающего в каждом индивидуальном задании три конкретных значения.

2. В качестве шумового сигнала в курсовой работе рассматривается стационарный случайный дискретный процесс, представляющий собой последовательность отсчетов, являющихся значениями непрерывной нормально распределенной случайной величины  с заданными значениями математического ожидания  и дисперсии.  Здесь  - интервал дискретизации, а  - среднеквадратичное значение

3.Задание на курсовую работу заключается в следующем:

а) рассчитать спектральные функции для одного варианта заданного входного сигнала, выбрать по указанному в индивидуальном задании критерию один из них и провести его дискретизацию;

б) методом билинейного z-преобразования синтезировать дискретный фильтр (ДФ) нижних частот (ФНЧ) с частотой среза, где  - частота, на которой уровень амплитудного спектра  выбранного входного видеосигнала снижается до уровня  спектра выбранного входного сигнала . При этом в качестве аналогового прототипа используется ФНЧ с максимально плоской амплитудно-частотной характеристикой (АЧХ) - фильтр Баттерворта, обеспечивающий на удвоенной частоте среза аналогового фильтра  затухание не менее ;

в) рассчитать амплитудно-частотную и импульсную характеристики синтезированного ДФ;

г) определить вид дискретных сигналов на выходе фильтра при воздействии на его вход последовательности отсчетов входного сигнала , а также двух-трех сигналов стандартной формы (заданных преподавателем);

д) выполнить анализ прохождения через синтезированный фильтр случайного дискретного сигнала с оценкой его математического ожидания, дисперсии, корреляционной функции и интервала корреляции на входе и выходе ДФ. Исследовать фильтрацию аддитивной смеси исходных дискретных детерминированного и случайного сигналов при различных значениях отношения сигнал/шум на входе ДФ.

Задание на курсовую работу.

Таблица 1

Фильтр			Сигнал								Критерий
			Время, мкс				Напряжения, В
Тип

Аналитическая форма задания сигнала :

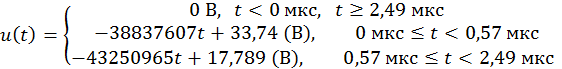
График нашего сигнала представлен на рисунке 1.

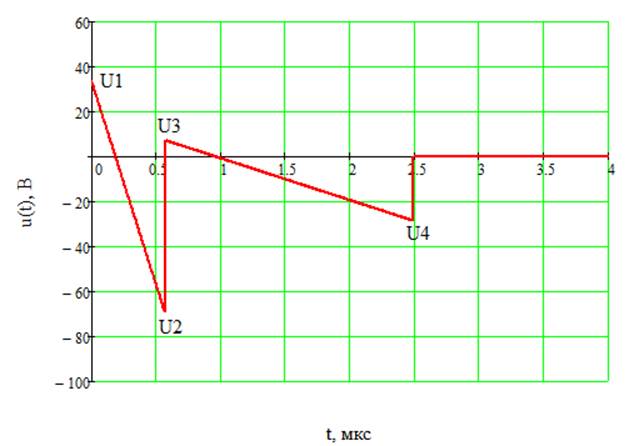
Рис.1. График исходного сигнала.

1. Расчёт спектральных характеристик сигнала.

1.1 Вывод аналитического выражения для спектральной функции сигналов.

Если модель финитного сигнала представлена кусочно (на отдельных интервалах) или полностью только функциями вида

то для вычисления его спектральной функции целесообразно применение процедуры - кратного дифференцирования  с последующим определением спектра производной  и, с использованием оператора интегрирования в частотной области  Продифференцировав первый и второй раз исходный сигнал, получаем следующее (рис.2 и 3 соответственно)

Рис.2. Первая производная исходного сигнала.

Рис 3. Вторая производная исходного сигнала.

Таким образом, вторая производная сигнала имеет вид

Преобразование Фурье сигнала :

Следовательно,

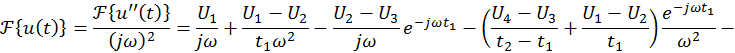
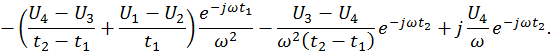
Представим спектральную функцию в виде

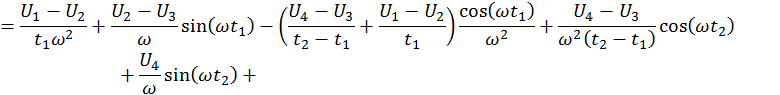
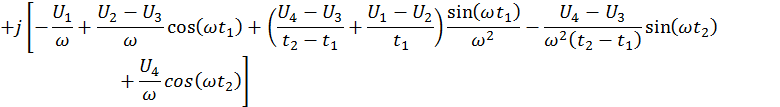
Таким образом,

1.2 Аналитическое определение значений действительной и мнимой части спектральной функции в нуле.

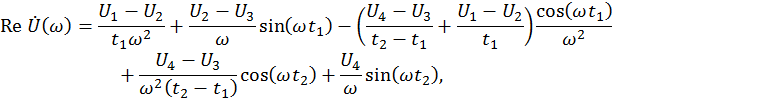
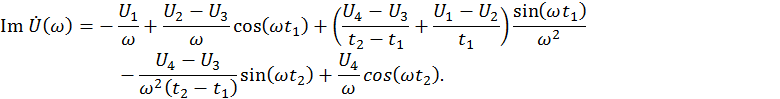
Расчёт для действительной части.

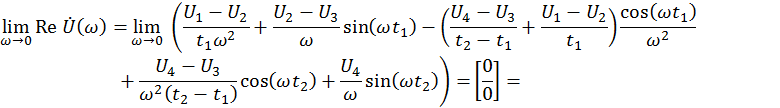
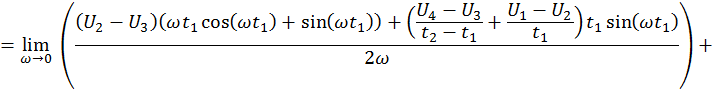
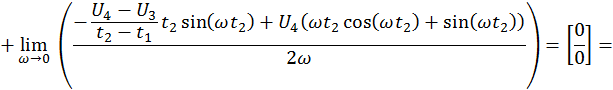
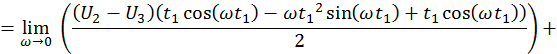
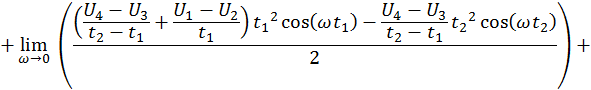
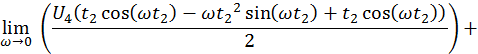
Таким образом,

Для

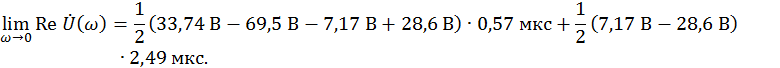
Для

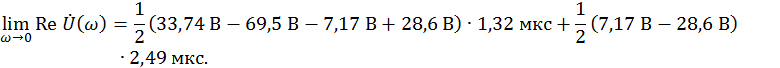
Для

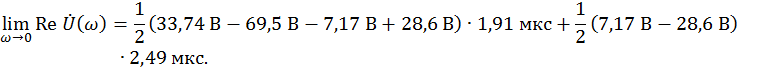
Учитывая, что , то на рисунках 4, 5, 6 соответственно, мы можем убедиться в верности найденных выше пределов.

Расчёт для мнимой части.

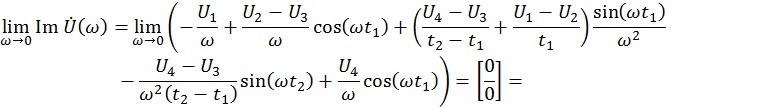
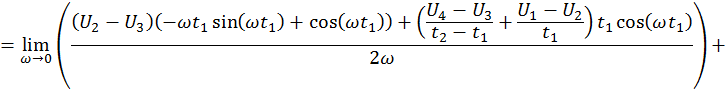
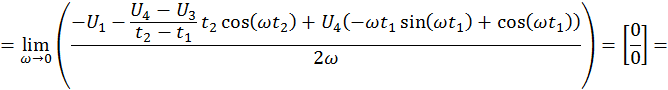
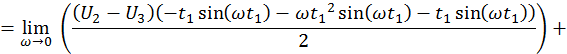
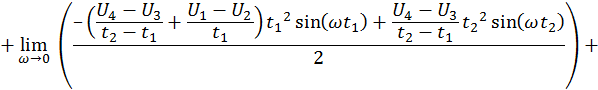
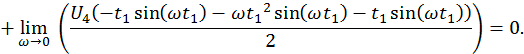
Таким образом

1.3 Расчёт модуля спектральной функции.

Спектральную функцию сигнала можно представить в следующем виде

где  - амплитудный спектр сигнала,  - его фазовый спектр, причём

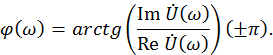
Графики амплитудных спектров для , ,  представлены соответственно на рисунках 4, 5 и 6.

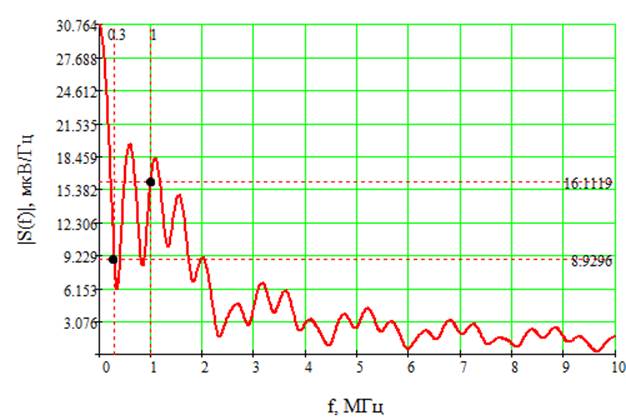
Рис.4. АС сигнала при

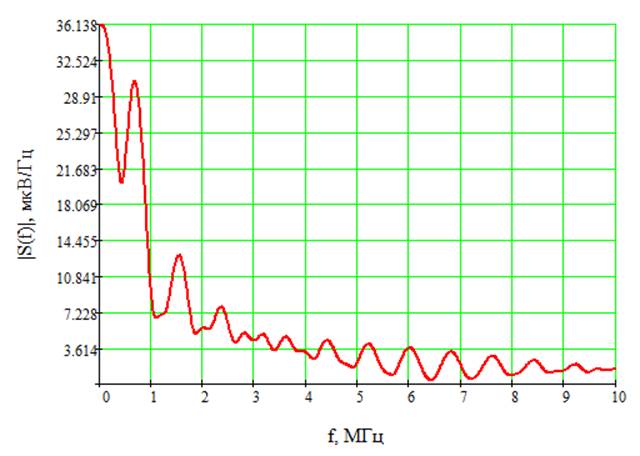
Рис.5 АС сигнала при

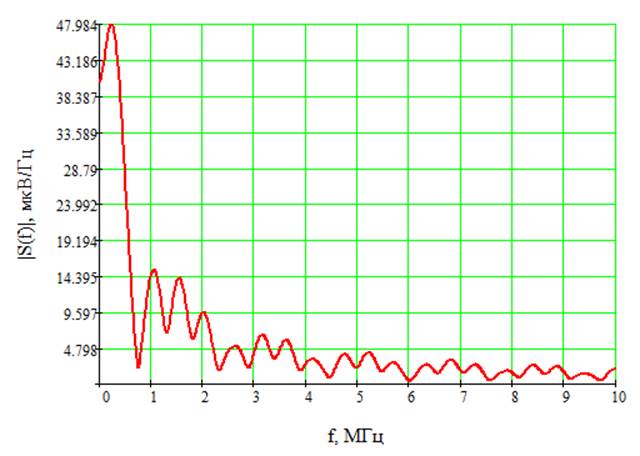
Рис.6 АС сигнала при

С помощью функции «трассировка» в приложении MathCad определяем частоту, на которой значение  составит 10% от максимального. Получаем следующие результаты:

Исходя из критерия средней граничной частоты, делаем вывод, что удовлетворяющая нас частота равна

Таким образом, в дальнейшем будем использовать значение времени

1.4 Расчёт фазового спектра.

Выражение для фазового спектра имеет вид

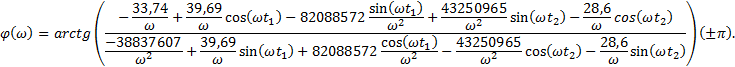
График для фазового спектра представлен на рисунке 7.

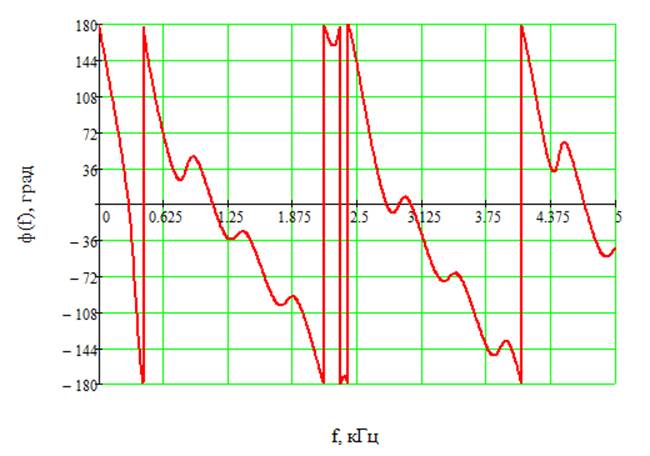
Рис.7 Фазовый спектр сигнала.

1.5 Контрольный ручной расчёт.

Произведём расчёт для  и .

Для .

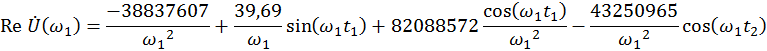
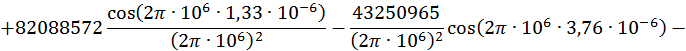
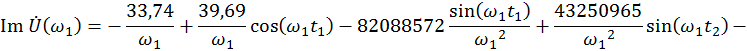
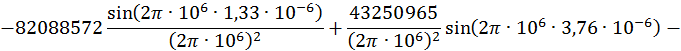
Для .

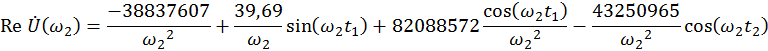
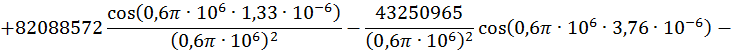
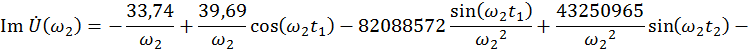
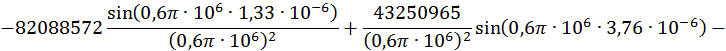
В правильности найденных нами значений мы можем убедиться, если посмотрим на график АС исходного сигнала, изображённого на рисунке 4.

2.Дискретизация аналогового сигнала.

2.1 Определение интервала дискретизации и расчёт последовательности отсчётов аналогового сигнала.