Синтез и анализ дискретного фильтра, выполненного на основе аналогового фильтра Батерворта, страница 3

Для того чтобы рассчитать импульсную характеристику из системной функции, необходимо, чтобы системная функция была правильной дробно-рациональной функцией, т. е. степень числителя должна быть меньше степени знаменателя, т.е.

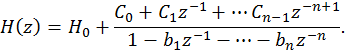
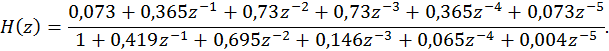
Из неправильной дроби выделяется целая часть, равная отношению коэффициентов при старших степенях z, т.е. функция  записывается в форме

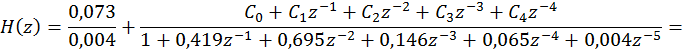
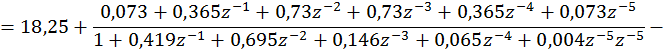
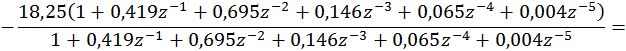
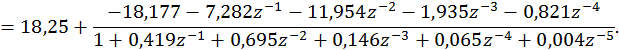
Знаменатель второго слагаемого необходимо разложить на множители следующего вида , где  - полюса системной функции. Таким образом, имеем следующее выражение для системной функции:

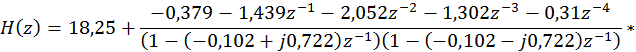
Второе слагаемое необходимо разложить на сумму простейших дробей, т.е

и сопоставить их со вторым слагаемым. Т.о.

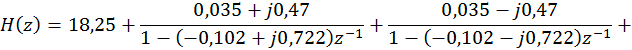
Первому слагаемому соответствует слагаемое импульсной характеристики вида

Здесь  - единичный дискретный сигнал. Остальные пять слагаемых представляют собой суммы бесконечных геометрических прогрессий:

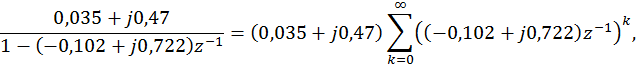
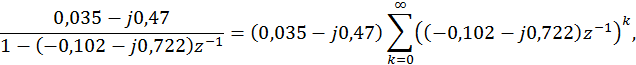
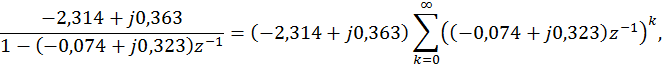
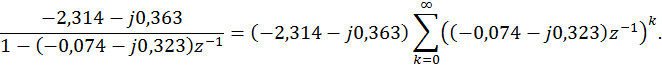
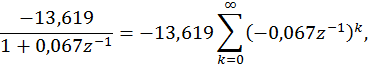
Для удобства записи комплексные коэффициенты целесообразно представить в экспоненциальной форме:

Полная импульсная характеристика рассматриваемого дискретного фильтра представляет собой сумму полученных слагаемых:

Полученное выражение является вещественным, но содержит два комплексно-сопряженных слагаемых. Поэтому в качестве последнего шага от этих слагаемых нужно избавиться, суммируя их по формуле Эйлера:

В таблице 3 отражены значения импульсной характеристики для 20 отсчётов.

Таблица 3

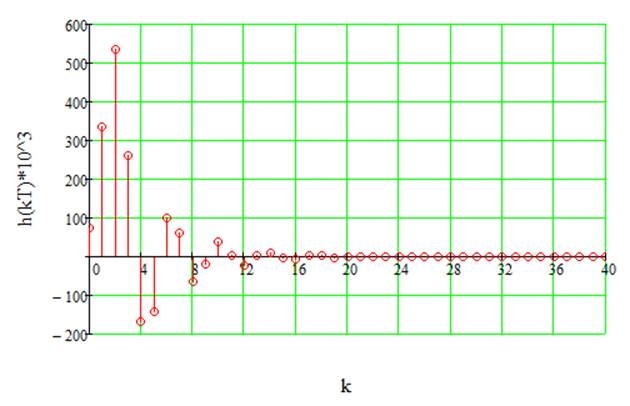
Рис.12. Последовательность отсчётов ИР ДФ.

3.7 Контроль полученной импульсной реакции.

Разностное уравнение дискретного фильтра согласно его системной функции имеет следующий вид:

Для проверки ИР следует принять  и последовательно вычислить несколько отсчетов  при различных , которые должны совпасть со значениями, вычисленными для тех же  по аналитической формуле.

Для :

Для :

Для :

Для :

Для :

Для :

Легко видеть, что результаты, представленные в таблице 3 и те результаты, которые мы получили при ручном расчёте, имеют небольшое отклонение, поэтому можно с уверенностью утверждать, что полученное выражение для импульсной характеристики является верным.

4. Реализация структурной схемы ДФ.

4.1 Синтез структурной схемы ДФ.

4.1.1 Основная форма.

Для построения прямой схемы реализации дискретного фильтра алгоритм дискретной фильтрации должен быть представлен в следующем виде:

Рис. 13 Прямая схема реализации ДФ.

4.1.2 Каноническая форма ДФ.

Для представления в канонической форме необходимо выражение для системной функции представить в форме  где

Далее независимо синтезировать структурные схемы для системных функций  и  в прямой форме и соединить их каскадно. При этом используют разностные уравнения, которые для указанных функций будут иметь вид:

 

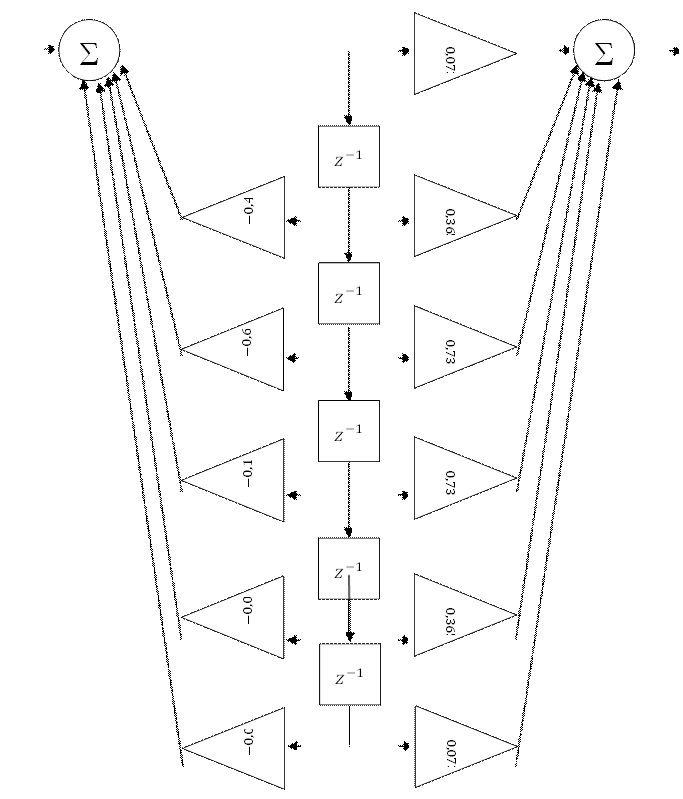Рис.14 Каноническая форма ДФ.

4.1.3 Параллельная форма ДФ.

Реализация параллельной схемы ДФ производится при представлении исходной системной функции в виде суммы нескольких парциальных системных функций:

каждая из которых соответствует дискретному фильтру порядка не выше второго (порядок фильтра равен числу полюсов его системной функции). Тогда нашу системную функцию можно представить следующим образом: