Синтез и анализ дискретного фильтра, выполненного на основе аналогового фильтра Батерворта, страница 2

Интервал дискретизации T вычисляют по следующей формуле

при этом коэффициент  необходимо подобрать таким образом, чтобы на длительность входного сигнала приходилось 20 отсчётов. Тогда

Следовательно, интервал дискретизации

Положив , где , получаем дискретизацию сигнала, что отображено в таблице 2 и на рисунке 8.

Таблица 2

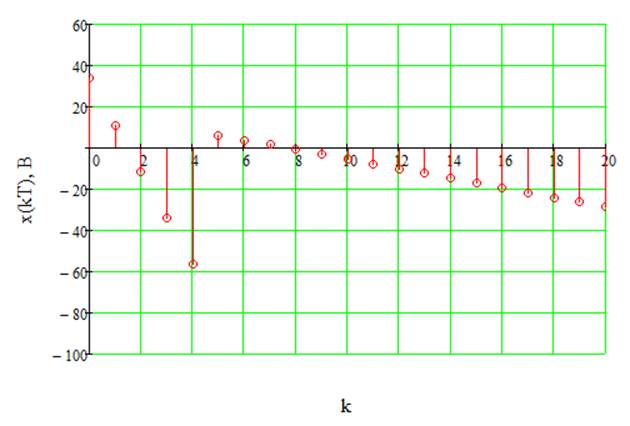
Рис.8 Дискретизация исходного сигнала.

2.2 Запись аналитического выражения для спектральной функции ДС.

Аналитическое выражение для спектральной функции дискретизированного сигнала

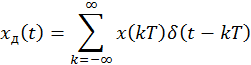
записывается следующим образом:

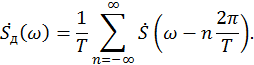
Исходя из этого выражения, мы можем построить график модуля спектральной функции . Он изображён на рисунке 9.

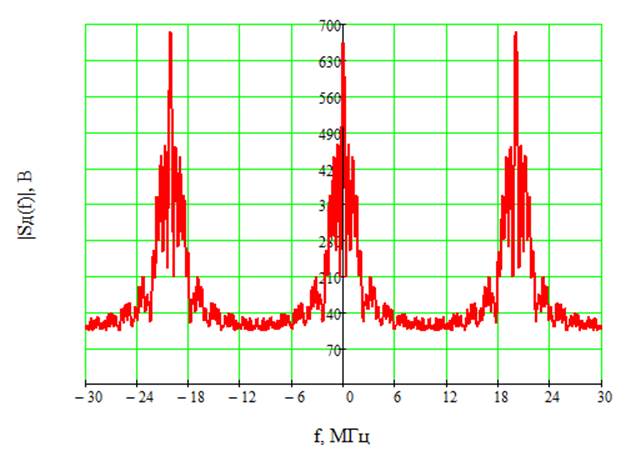
Рис.9 Амплитудный спектр дискретизированного сигнала.

Мы видим, график модуля спектральной функции  дискретизированного сигнала является периодическим повторением спектра непрерывного сигнала.

3. Определение параметров АЧХ аналогового фильтра-прототипа. Определение системной функции и параметров ДФ.

3.1 Определение порядка аналогового фильтра-прототипа.

Для определения АЧХ фильтра Баттерворта, необходимо знать частоту среза и порядок фильтра.

Частота среза вычисляется, исходя из следующего выражения

где - интервал дискретизации, .

Порядок аналогового фильтра определяется из условия обеспечения необходимого затухания a его АЧХ на удвоенной частоте среза. Это условие записывается таким образом:

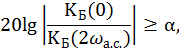
где  - АЧХ фильтра Баттерворта.

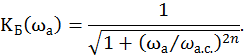
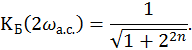
Таким образом

Следовательно, порядок фильтра

3.2 Запись аналитического выражения для функции передачи.

Выражение для функции передачи, исходя из того, что наш фильтр имеет 5 порядок, имеет следующий вид:

где .

3.3 Вывод аналитического выражения для системной функции.

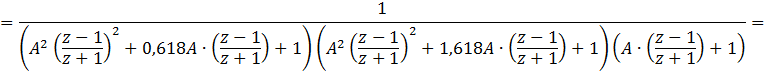
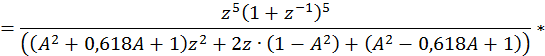
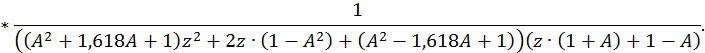
Из этого выражения следует, что

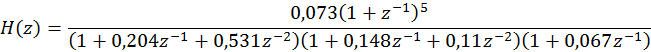
Представим системную функцию в следующем виде

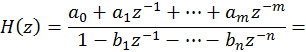
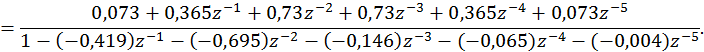
Должно выполняться следующее условие

Проверка сходится!

3.4 Анализ устойчивости ДФ с найденной системной функцией.

Чтобы выяснить, является ли устойчивым ДФ, необходимо найти полюса системной функции и убедиться, что они не выходят за пределы единичной окружности. Чтобы найти полюса, необходимо знаменатель системной функции прировнять к нулю, положить и решить уравнения.

Первое уравнение:

Таким образом ,, .

Второе уравнение:

Таким образом ,, .

Третье уравнение

На рисунке 10 отмечены полюса системной функции.

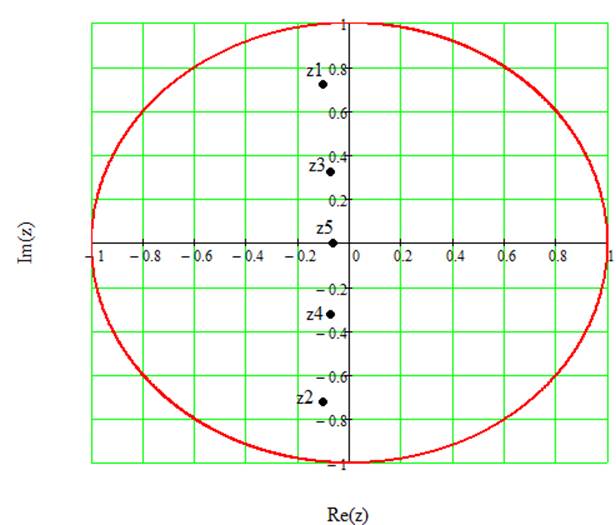
Рис.10 Полюса системной функции на комплексной плоскости переменной z.

Полюса не выходят за пределы единичной окружности, следовательно, фильтр устойчив.

3.5 Запись аналитического выражения и расчёт АЧХ дискретного фильтра

Известная системная функция дискретного фильтра позволяет, определить его АЧХ:

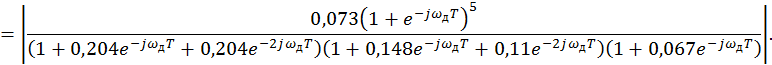
АЧХ аналогового фильтра выглядит следующим образом

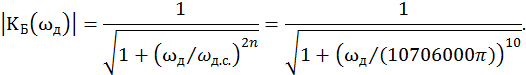
Графики аналогового и дискретного фильтров изображены на рисунке 11.

1 – дискретный фильтр.

2 - аналоговый фильтр-прототип.

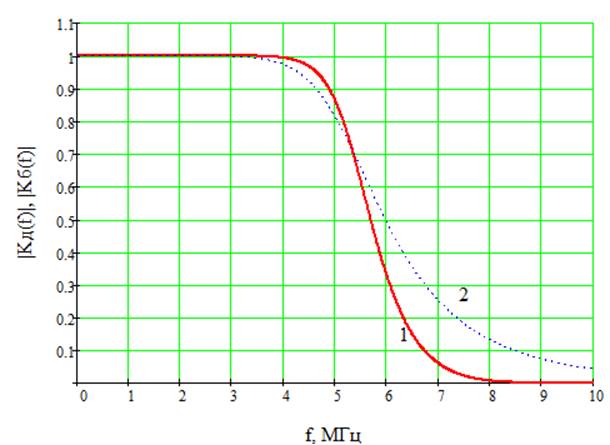
Рис.11 АЧХ дискретного фильтра и аналогового фильтра-прототипа.

3.6 Вывод аналитического выражения для импульсной реакции ДФ.