Другие предметы \ Математический аппарат радиотехники

Множество и операции над множествами. Декартово произведение множеств. Определение понятия равенства двух множеств Исчерпывающее описание случайной величины. Плотность вероятности случайной величины, страница 2

Если бинарная операция является коммутативной, то группа называется абелевой.

  1. Какая алгебраическая структура называется кольцом?

Если по  отношению к операции сложения мы имеем абелеву группу, а по отношению к операции умножения – моноид, и операции сложения и умножения связаны законом дистрибутивности, то такая алгебраическая структура называется кольцом.

  1. Что такое поле? Какие поля называют полями Галуа?

Если по отношению к операции сложения и умножения мы имеем  абелеву группу, то кольцо превращается в поле. Операции сложения и умножения связаны законом дистрибутивности. Поля, заданные на конечных множествах, называют полями Галуа и обозначают как GF(n), где п – число элементов множества

  1. Что такое метрическое пространство?

Множество Х элементов различной природы образует метрическое пространство, если любой паре элементов xi, xj, принадлежащих данному множеству (xi, xj ÎХ), поставлено в соответствие (определено) неотрицательное вещественное число  r (xi, xj), называемое расстоянием между элементами xi и  xj. Символически сформулированное определение записывается как (Х, r).

  1. Каким аксиомам должно удовлетворять расстояние между элементами множества?

1.  r (xi, xj) = 0 только, если xi = xj.

При задании на одном и том же множестве Х различных метрик, из равенства нулю расстояния между элементами в одной метрике не следует равенства нулю расстояния в другой.

2. r (xi, xj) = r (xj, xi). Это утверждение называют аксиомой симметрии.

3.  Для любых xi, xj, xk ÎХ  r (xi, xk) £ r (xi, xj) + r (xj, xk).

  1. Как определяется расстояние между векторами в евклидовом пространстве?

  - n-мерный вектор  =(). , - n-мерное вещественное (действительное) евклидово пространство . Евклидово расстояние с весом, определяемым вектором  с неотрицательными компонентами  .

Евклидово пространство  может быть обобщено на случай бесконечномерных векторов = (, …), где Î R и выполняется условие 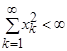. Расстояние между векторами данного пространства определяется формулой , а оно само обозначается как l2.

  1. Что называется нормой элемента векторного пространства?

Нормой элемента  произвольного векторного пространства Х, обозначаемой как ||||, называют неотрицательное вещественное число, причем способ отображения Х в множество R+ (множество неотрицательных вещественных чисел) должен удовлетворять следующим условиям:

1.  |||| = 0, только если  = ;

2.  ||a|| = |a| × |||| , где a – скаляр;

3.  || +|| £ |||| + |||| (неравенство треугольника).

  1. Сформулируйте аксиомы линейного пространства.

1.Для любых ,  Î L однозначно определен  элемент  Î L, называемый суммой элементов  и , т. е. =+. При этом по отношению к введенной операции сложения векторов L образует абелеву группу.

2.Для " a Î Fи Î L определен элемент aÎ L(произведение вектора на скаляр), причем:

А. a(b) = (ab);

Б. е = , где е – нейтральный элемент по отношению к операции умножения в поле F (е = 1 для поля комплексных и вещественных чисел);

В.  для " a, b Î Fвыполняется равенство (a + b) = a + b;

Г. ",  Î L и a Î F  a(+) = a + a.

  1. При каком условии ненулевые вектора являются линейно зависимыми?

Ненулевые вектора 1, 2, …, n называются линейно зависимыми, если существуют не все равные нулю скаляры a1, a2, …, aп такие, что .

  1. В каком случае совокупность векторов образует базис пространства?

Если в L существует п линейно независимых векторов 1, 2, …, n, а любые n + 1 векторов линейно зависимы, то число n называют размерностью пространства L , записывая это утверждение в форме dim L = n. Сами вектора 1, 2, …, n образуют базис п-мерного ЛП L.

  1. Каковы основные свойства базиса?
Скачать файл