Например, при переходе от
декартовых координат к полярным, этот случай нам потребуется в дальнейшем,
случайные величины ![]() и
и ![]() ,
радиус-вектор и полярный угол, связаны со случайными величинами
,
радиус-вектор и полярный угол, связаны со случайными величинами ![]() и
и ![]() , декартовы
координаты, известными соотношениями
, декартовы
координаты, известными соотношениями ![]() =
=![]() и
и
![]() =
=![]() . Соответственно,
. Соответственно, ![]() и
и ![]() .
Вычисляя якобиан, получим
.
Вычисляя якобиан, получим 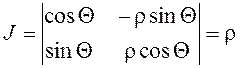 и ПВ полярных координат
и ПВ полярных координат
![]() ,
, ![]() связана
с ПВ декартовых координат
связана
с ПВ декартовых координат ![]() =
=![]() ,
,
![]() =
=![]() соотношением
соотношением
![]() .
.
Знак модуля в данном случае можно опустить,
так как ![]() .
.
Обобщение на случай
многозначности решений системы уравнений, задающей связь между СВ ![]() и
и ![]() выглядит
аналогично одномерному случаю
выглядит
аналогично одномерному случаю
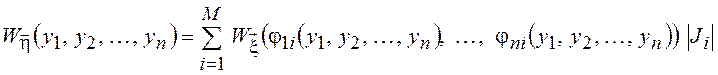 ,
,
где ![]() – число
решений.
– число
решений.
Полученные результаты
позволяют сравнительно просто решать задачу определения ПВ случайной величины,
являющейся функцией нескольких СВ. Пусть ![]() =
=![]() и ПВ
и ПВ ![]() известна.
Введем СВ
известна.
Введем СВ ![]() по правилу
по правилу ![]() =
=![]() ,
, ![]() =
=![]() , …,
, …, ![]() =
=![]() и запишем в соответствии с полученными
результатами
и запишем в соответствии с полученными
результатами
![]() ,
,
где 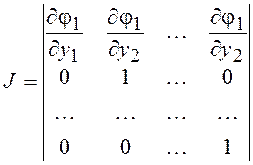 =
=![]() . Для отыскания ПВ случайной величины
. Для отыскания ПВ случайной величины ![]() необходимо проинтегрировать полученное
выражение по всем значениям
необходимо проинтегрировать полученное
выражение по всем значениям ![]() , т. е.
, т. е.
![]() =
=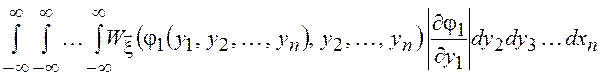 .
.
Рассмотрим конкретные и очень важные примеры.
2.1. Распределение суммы СВ
Пусть ![]() =
=![]() +
+![]() ,
, ![]() =
=![]() , тогда
, тогда ![]() =
=![]() ,
, 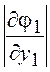 =1 и мы
получим
=1 и мы
получим ![]() =
=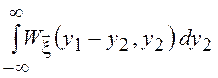 , что естественно
совпадает с полученным ранее выражением. Для ПВ разности СВ
, что естественно
совпадает с полученным ранее выражением. Для ПВ разности СВ ![]() =
=![]() –
–![]() аналогично
получим
аналогично
получим ![]() =
=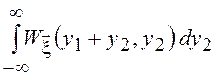 .
.
2.2. Распределение произведения СВ
Пусть ![]() =
=![]()
![]() ,
, ![]() =
=![]() . Тогда
. Тогда ![]() =
=![]() ,
, 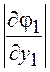 =
=![]() и
и ![]() =
=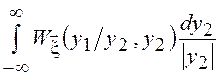 .
.
2.3. Распределение частного СВ
Пусть ![]() =
=![]() ,
,
![]() =
=![]() . Аналогично предыдущим
случаям
. Аналогично предыдущим
случаям ![]() =
=![]() ,
, 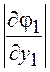 =
=![]() и
и ![]() =
=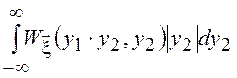 .
.
Как будут выглядеть эти формулы для независимых СВ, догадаться нетрудно.
Контрольные вопросы
1. Как формулируется задача отыскания ПВ функционально преобразованных СВ?
2. Как находится ПВ
случайной величины ![]() , если известна совместная ПВ
случайных величин
, если известна совместная ПВ
случайных величин ![]() и
и ![]()
![]() ? Как выглядит этот результат, если СВ
? Как выглядит этот результат, если СВ ![]() и
и ![]() независимы?
независимы?
3. Дайте определение
характеристической функции СВ ![]() ; случайного вектора
; случайного вектора ![]() .
.
4. Сформулируйте свойства ХФ.
5. Как решается задача
отыскания ПВ случайной величины ![]() , если известна ПВ
, если известна ПВ ![]() ?
?
6. Пусть СВ ![]() описывается нормальным распределением
описывается нормальным распределением 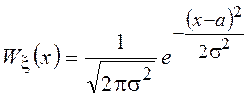 . Найти ПВ случайной величины
. Найти ПВ случайной величины ![]() , если
, если ![]() ;
; ![]() ;
; ![]() ,
, 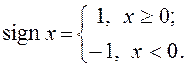
7. Как решается задача определения ПВ функционально преобразованной совокупности СВ?
8. Декартовы координаты точки ![]() и
и
![]() являются СВ, описываемыми совместной ПВ
являются СВ, описываемыми совместной ПВ ![]() . Записать выражения для ПВ длины
. Записать выражения для ПВ длины ![]() и аргумента
и аргумента ![]() случайного
вектора, начало которого находится в точке (0,0), а конец в точке
случайного
вектора, начало которого находится в точке (0,0), а конец в точке ![]() .
.
9. Как решается задача об
отыскании ПВ случайной величины ![]() при заданной ПВ
при заданной ПВ ![]() ?
?
10. Найдите ПВ суммы и
разности независимых нормальных СВ, имеющих параметры ![]() ,
,
![]() и
и ![]() ,
, ![]() соответственно.
соответственно.
Глава 3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Рассмотренные ранее функция распределения, плотность вероятности и характеристическая функция дают наиболее полное представление о СВ. Однако, являясь функциями одной или нескольких переменных, для многомерных СВ, они представляют собой достаточно сложные объекты. Во многих случаях достаточно бывает использовать для описания СВ совокупность чисел, называемых числовыми характеристиками СВ. Познакомимся с этими числовыми характеристиками.
3.1. Моменты случайной величины
Под начальным ![]() -м моментом СВ
-м моментом СВ ![]() , где
, где ![]() = 1, 2, … понимают величину
= 1, 2, … понимают величину 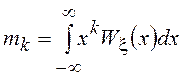 , где особую роль играет
, где особую роль играет 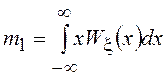 , называемый математическим ожиданием или
средним значением СВ
, называемый математическим ожиданием или
средним значением СВ ![]() . Моменты СВ
. Моменты СВ ![]() существуют тогда и только тогда, когда
существуют тогда и только тогда, когда 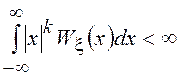 ,
, ![]() = 1,
2, …. Часто для записи математического ожидания используют символ статистического
усреднения, обозначаемый М, Е или просто прямой чертой сверху, т. е.
= 1,
2, …. Часто для записи математического ожидания используют символ статистического
усреднения, обозначаемый М, Е или просто прямой чертой сверху, т. е.
![]() ,
, ![]() или
или ![]() . Для дискретных СВ, задаваемых
распределением (
. Для дискретных СВ, задаваемых
распределением (![]() ),
), ![]() = 1, 2, …,
= 1, 2, …, ![]() , математическое ожидание равно
, математическое ожидание равно 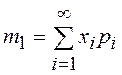 , если записанный ряд сходится абсолютно.
, если записанный ряд сходится абсолютно.
Используя аппарат дельта-функций, для дискретных СВ можно пользоваться интегральной формой записи математического ожидания
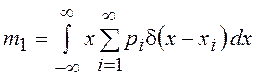 =
=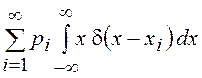 =
=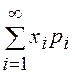 .
.
[*] В дальнейшем для краткости записи, если будет ясно, о какой СВ идет речь, индекс у ФР и ПВ будет опускаться.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.