Математический аппарат радиотехники. Часть II. Случайные процессы: Учебное пособие, страница 3

Пусть проведено  испытаний и нас интересует, какова вероятность того, что успех имел место ровно  раз, где . Рассмотрим элементарные события, соответствующие этой задаче. Если обозначить успех как 1, а неудачу как 0, то элементарные события есть N‑мерные векторы вида , , …,, в которых появление 1 на -й позиции означает завершение -го испытания успехом. Вероятность каждого элементарного события определяется числом единиц и нулей, входящих в соответствующий вектор, и в соответствии с независимостью испытаний равна, где  – число единиц (успехов), а  – число нулей (неудач). Вероятность элементарного события, благоприятствующего наступлению интересующего нас случайного события (ровно  успехов в  испытаниях) равна . Число таких элементарных событий есть , поэтому искомая вероятность будет равна  и определяет биномиальное распределение. Функция распределения и ПВ рассматриваемой СВ имеют вид соответственно

, .

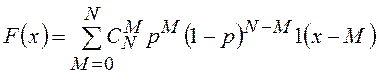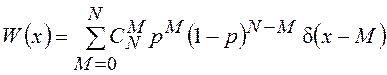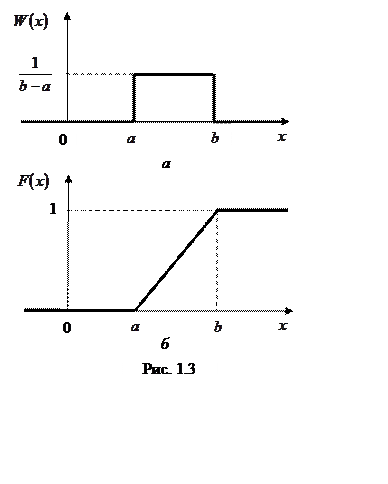
1.3. Равномерное распределение

Случайная величина  имеет на отрезке  равномерное распределение, если ее ПВ

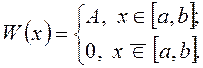
Величина  определяется из условия нормировки 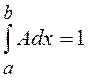 и равна 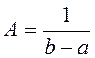. Функция распределения очевидно равна

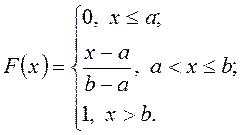
Графики ПВ и ФР равномерно распределенной СВ приведены на рис. 1.3.

1.4. Нормальное распределение

Нормальное или гауссовское распределение играет фундаментальную роль в теории вероятностей и ее приложениях благодаря тому, что при весьма широких предположениях сумма независимых случайных величин с ростом числа слагаемых ведет себя асимптотически нормально.

Простейшее утверждение такого рода, называемое локальной предельной теоремой, или теоремой Муавра, связано с рассмотренным выше биномиальным распределением и звучит следующим образом.

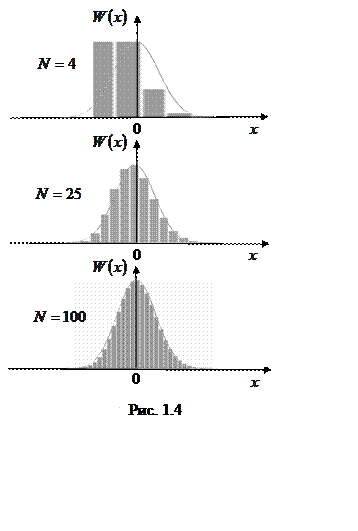
Если вероятность наступления события при  последовательных независимых испытаниях постоянна и равна : (), то вероятность  того, что событие будет иметь место ровно  раз, удовлетворяет в пределе соотношению

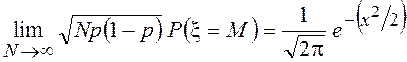
равномерно для всех , для которых 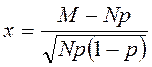 находится в каком-либо конечном интервале. Доказательство этого факта, опирающееся на формулу Стирлинга, можно найти в [1].

Для иллюстрации на рис. 1.4 приведены графики для биномиального распределения, у которого используется
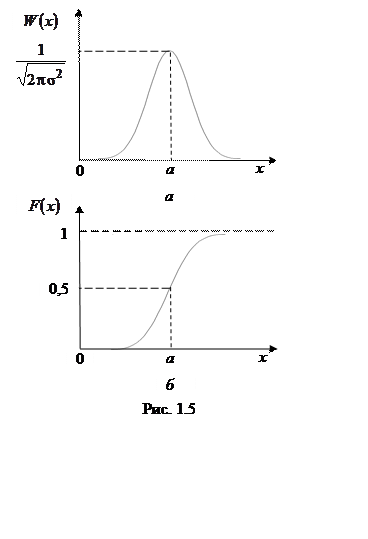
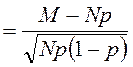 по оси абсцисс вместо , а по оси ординат  соответственно  , а также аппроксимирующая функция 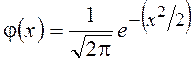. Хорошо видно повышение качества аппроксимации с ростом .

Интегральная теорема Муавра–Лапласа утверждает, что в сформулированных ранее условиях (условия локальной предельной теоремы)

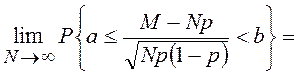
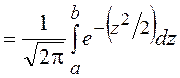
равномерно относительно  и  ().

Общая форма записи ПВ нормальной СВ имеет вид

.

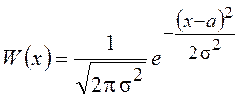Смысл параметров  и  будет выяснен позже.

Функция распределения нормальной СВ может быть выражена через рассмотренный в главе 6 первой части пособия интеграл вероятностей

.

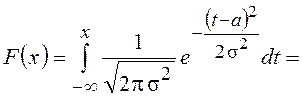
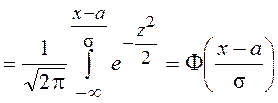На рис. 1.5 приведены графики ПВ (а) и ФР (б) нормальной СВ.

1.5. Многомерные или векторные СВ

Случайным называется вектор , компоненты которого  (координаты относительно ортонормального базиса) 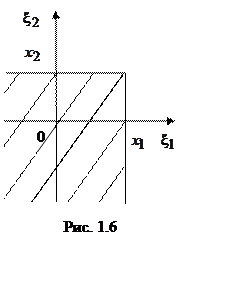есть СВ. Случайный вектор =, называемый также -мерной случайной величиной, полностью характеризуется -мерной ФР, определяемой как вероятность произведения случайных событий , т. е. ==.

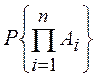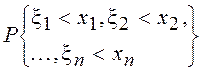Естественно рассматривать  как координаты точек -мерного евклидова пространства  или C. Тогда  дает вероятность попадания точки () в -мерный параллелепипед с ребрами, параллельными осям координат. Например,  есть вероятность попадания точки () в заштрихованную область (рис. 1.6).

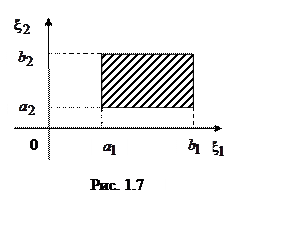
С помощью ФР можно легко вычислить вероятность попадания точки () в параллелепипед  (). Например,  =  (рис. 1.7). В общем случае [1]

=

=,

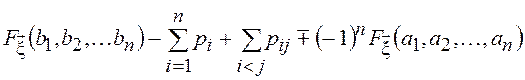где через  обозначено значение функции  при , ,  и при остальных .

Если часть переменных функции  равна , т. е. эти переменные могут принимать любые значения, мы будем иметь ФР остальных не равных  переменных. Например,  = ,  = .