Глава 2. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Поставим
следующую задачу. Пусть многомерная СВ (случайный вектор) ![]() =
=![]() имеет ПВ
имеет ПВ ![]() и компоненты другого случайного вектора
и компоненты другого случайного вектора ![]() =
=![]() функционально связаны
с компонентами вектора
функционально связаны
с компонентами вектора ![]() , т. е.
, т. е. ![]() ,
, ![]() , … ,
, … , ![]() . Тогда ФР случайного вектора
. Тогда ФР случайного вектора ![]() =
=![]()
![]()
![]() =
=![]()
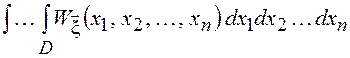 ,
,
где область ![]() определяется
неравенствами
определяется
неравенствами ![]() ,
, ![]() .
.
Пример. Пусть требуется найти ФР и ПВ суммы
СВ ![]() , т. е.
, т. е. ![]() . В
соответствии со сказанным ФР случайной величины
. В
соответствии со сказанным ФР случайной величины ![]()
![]() есть вероятность попадания точки (
есть вероятность попадания точки (![]() ) в подпространство
) в подпространство ![]() ,
или
,
или
![]()
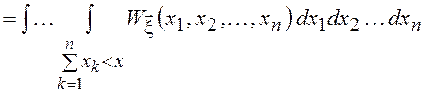 .
.
 Для
Для ![]() это даст
это даст ![]() =
=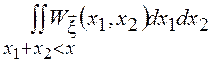 .
.
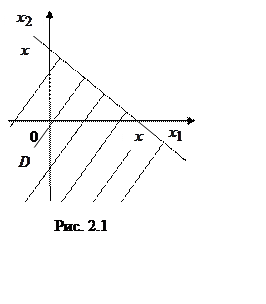
Область интегрирования представлена на рис. 2.1.
Переходя от двойного интеграла к повторному, получим
![]()
![]() =
=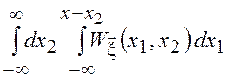 .
.
Для отыскания ПВ суммы СВ
![]() и
и ![]() , считая
записанный интеграл дифференцируемым по параметру
, считая
записанный интеграл дифференцируемым по параметру ![]() , получим
, получим
![]()
![]() =
=![]()
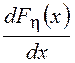
![]() =
=![]()
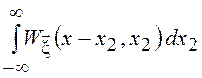 .
.
Если СВ ![]() и
и ![]() независимы, то
независимы, то ![]()
![]() =
=![]()
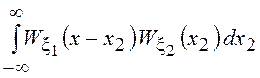 ,
где
,
где ![]() и
и ![]() – ПВ
случайных величин
– ПВ
случайных величин ![]() и
и ![]() соответственно.
Таким образом, для независимых СВ, для которых
соответственно.
Таким образом, для независимых СВ, для которых ![]() =
= ![]()
![]() ,
ПВ суммы есть свертка ПВ слагаемых
,
ПВ суммы есть свертка ПВ слагаемых ![]() .
.
Учитывая, что Фурье-образ
свертки есть произведение преобразований Фурье сворачиваемых функций,
целесообразно ввести в рассмотрение преобразование Фурье ПВ, что возможно, так
как для любой ПВ выполняется
условие абсолютной интегрируемости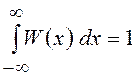 .
.
Определение. Преобразование Фурье ПВ ![]() определяет характеристическую функцию (ХФ)
СВ
определяет характеристическую функцию (ХФ)
СВ 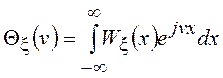 =
=![]() . Обратное преобразование
Фурье позволяет выразить ПВ через ХФ
. Обратное преобразование
Фурье позволяет выразить ПВ через ХФ
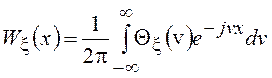 .
.
Различие знаков в показателе экспоненты для прямого и обратного преобразований по сравнению с обычно используемым несущественно, что и отмечено в гл. 5 первой части пособия.
Таким образом ХФ суммы
независимых СВ ![]() и
и ![]() есть
произведение ХФ слагаемых, т. е.
есть
произведение ХФ слагаемых, т. е. ![]() =
=![]()
![]() .
.
Характеристическая
функция естественно определяется и для многомерных СВ как многомерное преобразование
Фурье совместной ПВ случайных величин ![]()
![]()
![]() =
=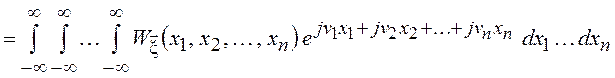 ,
,
![]() =
=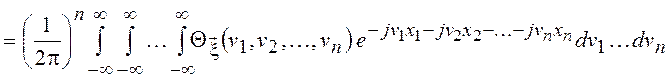 .
.
 Из определения многомерных ХФ видно, что если СВ
Из определения многомерных ХФ видно, что если СВ ![]() независимы, т. е.
независимы, т. е. ![]()
![]() =
=![]()
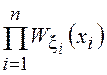 , то переменные в многомерном интеграле,
определяющем
, то переменные в многомерном интеграле,
определяющем ![]() , разделяются и
, разделяются и
![]()
![]() =
=![]()
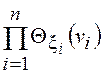 .
.
Вернемся к задаче отыскания ПВ функций от СВ. В рассмотренном примере мы показали, как можно найти ПВ функции от СВ (суммы) путем дифференцирования ФР. Однако можно решить задачу о нахождении ПВ функций от СВ, не обращаясь к помощи ФР.
Поясним это на примере.
Пусть требуется найти ПВ случайной величины ![]() ,
связанной со СВ
,
связанной со СВ ![]() функциональным соотношением
функциональным соотношением ![]() . Будем вначале считать, что
. Будем вначале считать, что ![]() задает взаимно однозначное соответствие между
СВ
задает взаимно однозначное соответствие между
СВ ![]() и
и ![]() (рис. 2.2).
(рис. 2.2).
Можно утверждать, что в
силу функциональной связи между ![]() и
и ![]() , вероятность попадания СВ
, вероятность попадания СВ ![]() в промежуток
в промежуток ![]() равна
вероятности попадания СВ
равна
вероятности попадания СВ ![]() в промежуток
в промежуток ![]() . Считая
. Считая ![]() и
и ![]() малыми, это утверждение можно записать в
виде
малыми, это утверждение можно записать в
виде ![]() . В пределе при
. В пределе при ![]() ,
,![]()
![]()
![]() это
равенство станет точным. Знак модуля ставится в силу неотрицательности вероятностей,
в то время как величины
это
равенство станет точным. Знак модуля ставится в силу неотрицательности вероятностей,
в то время как величины ![]() и
и ![]() , вообще говоря, имеют знак.
, вообще говоря, имеют знак.
 Разрешая уравнение
Разрешая уравнение ![]() относительно
относительно ![]() (в силу
наличия взаимно однозначного соответствия между
(в силу
наличия взаимно однозначного соответствия между ![]() и
и ![]() решение единственно)
решение единственно) ![]() и учитывая, что
и учитывая, что 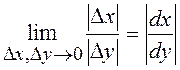 ,
получим окончательно
,
получим окончательно
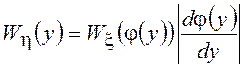 .
.
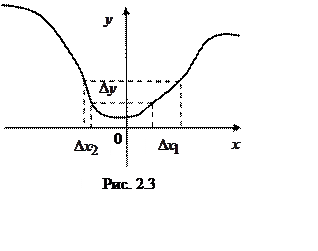
 Рассмотрим случай, когда уравнение
Рассмотрим случай, когда уравнение ![]() имеет несколько решений (рис. 2.3). В этом
случае вероятность попадания СВ
имеет несколько решений (рис. 2.3). В этом
случае вероятность попадания СВ ![]() в интервал
в интервал ![]() есть вероятность объединения двух несовместных
событий: попадание СВ
есть вероятность объединения двух несовместных
событий: попадание СВ ![]() в интервал
в интервал ![]() и попадание СВ
и попадание СВ ![]() в
интервал
в
интервал ![]() . Следовательно,
. Следовательно,
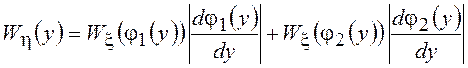 ,
,
где ![]() –
функции, обратные к fна
интервалах однозначности.
–
функции, обратные к fна
интервалах однозначности.
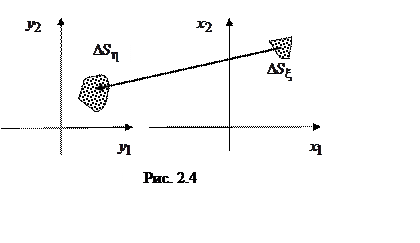
Двумерный случай иллюстрируется
рис. 2.4. Пусть связь СВ ![]() ,
, ![]() и
и ![]() ,
, ![]() задается функциями
задается функциями ![]() =
=![]() и
и ![]() =
=![]() и решения этой системы уравнений
и решения этой системы уравнений ![]() =
=![]() и
и ![]() =
=![]() . Вероятность попадания
СВ
. Вероятность попадания
СВ ![]() и
и ![]() в
область
в
область ![]() равна вероятности попадания СВ
равна вероятности попадания СВ ![]() и
и ![]() в область
в область
![]() , что с учетом малости областей
, что с учетом малости областей ![]() и
и ![]() можно записать как
можно записать как ![]() .
.
Знак модуля появился
вследствие того, что площади ![]() и
и ![]() ориентированы (направление обхода или
положение нормали). Переходя к пределу, получим
ориентированы (направление обхода или
положение нормали). Переходя к пределу, получим ![]() , где
, где 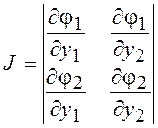 – определитель Якоби, или якобиан, имеющий
смысл масштабного коэффициента при преобразовании элемента площади из системы
координат
– определитель Якоби, или якобиан, имеющий
смысл масштабного коэффициента при преобразовании элемента площади из системы
координат ![]() в систему
в систему ![]() ,
связанных между собой записанными выше соотношениями
,
связанных между собой записанными выше соотношениями ![]() =
=![]() и
и ![]() =
=![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.