Математический аппарат радиотехники. Часть II. Случайные процессы: Учебное пособие, страница 2

СВ, для которой X – конечное или счетное множество, называется дискретной. Дискретную СВ можно полностью определить, задав распределение вероятностей, т. е. совокупность пар чисел , где  – значение СВ, а  – вероятность этого значения. Иногда распределение вероятностей называют рядом распределения, а графическое изображение ряда распределения – многоугольником распределения (фигура, полученная соединением ординат точек  ). Поскольку результатам = отвечают несовместные случайные события, образующие полную группу (все множество элементарных событий Ω), имеет место условие нормировки .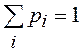

Для СВ, у которых X – континуальное множество, задание распределения вероятностей невозможно, так как вероятность определенного значения равна нулю.

Универсальным способом описания СВ любой природы является задание функции распределения (ФР), определяемой как вероятность события, состоящего в том, что СВ  будет меньше значения , являющегося аргументом функции распределения, т. е. .

Напомним свойства ФР.

1.  – неотрицательная неубывающая функция.

2. Функция  непрерывна слева, что символически можно записать как  –  = 0.

3. Функция распределения позволяет определить вероятность попадания СВ  в интервал  как =.

4. Функция  терпит разрыв первого рода при тех значениях , которые принимаются СВ  с конечной вероятностью . Величина скачка в точке разрыва равна вероятности . Функция распределения может иметь не более чем счетное множество скачков.

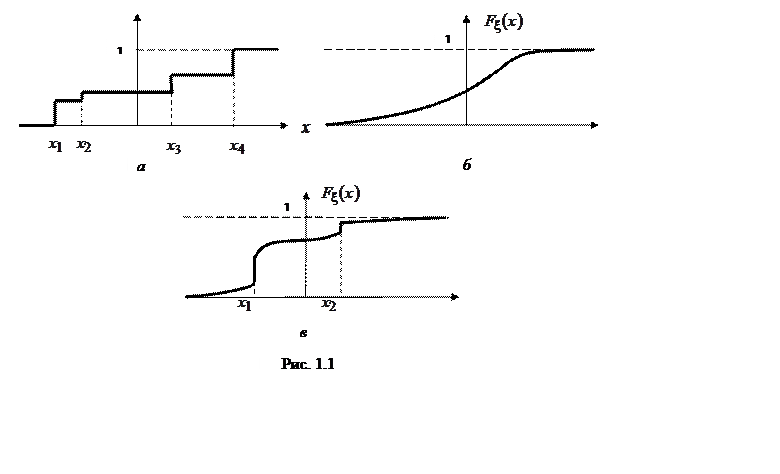
5. Значения  на левой и правой границах множества X, как вероятности невозможного и достоверного событий, равны соответственно нулю и единице. Поэтому,  = 0 и  = 1. На рис. 1.1 приведены ФР для СВ дискретного (а), непрерывного (б) и смешанного (в) типов.

Случайная величина называется непрерывной (относится к классу, типу непрерывных СВ), если существует неотрицательная функция , удовлетворяющая при любых  равенству

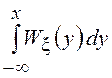 =, а .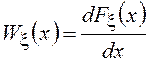

Функция  называется плотностью вероятности (ПВ).[*]

Напомним, что ПВ обладает следующими свойствами:

1.

2. При любых X справедливо равенство

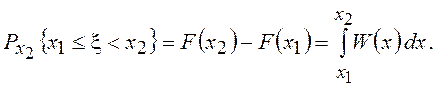
Если  непрерывна в точке , то с точностью до бесконечно малых высших порядков

.

Эта формула очень часто используется в вероятностных расчетах.

3. Следствием свойства 2 является условие нормировки

.

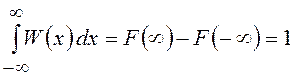Если ввести в рассмотрение обобщенные функции, то ПВ можно определить и для дискретных и смешанных типов СВ.

Например, ПВ случайной величины, для которой X состоит из  значений , имеет вид

,

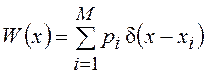где  – вероятность принятия значения .

Функция распределения при этом будет равна 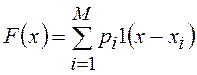, где

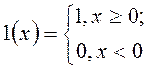
называется функцией единичного скачка, или функцией Хэвисайда. Неслучайная, детерминированная величина  имеет ПВ вида  и ФР .

Приведем примеры дискретных и непрерывных СВ и соответствующих им ФР и ПВ.

1.1. Распределение Бернулли

Случайная величина , описываемая распределением Бернулли с параметром  (), принимает значения  с вероятностью  и  с вероятностью . ФР такой СВ имеет вид

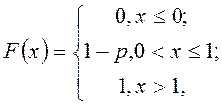
или , а ПВ равна .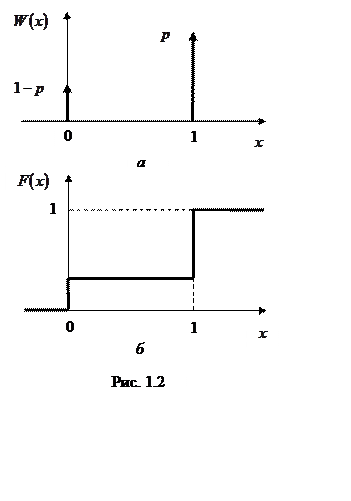

На рис. 1.2 приведены графики ПВ (а) и ФР (б).

Распределение Бернулли играет важнейшую роль в теории вероятностей и математической статистике, описывая статистическую модель с двумя исходами.

1.2. Биномиальное распределение

К биномиальному распределению мы приходим, рассматривая схему последовательных независимых испытаний. Предполагается, что испытания проводятся в неизменных условиях, вероятность успеха в каждом испытании равна  и не зависит от результатов предшествующих испытаний.