Исследование затухающих колебаний в колебательном контуре (лабораторная работа), страница 4

Их период определяется формулой Томсона:

                                                                                              (18)

Ток в контуре отстает по фазе от напряжения на величину . Начальная фаза и амплитуда колебаний определяются из начальных условий:

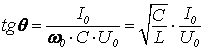                               ,                        (19)

б) β > ω_о. Оба корня  р_1,2  уравнения (6) действительны. Как видно из формулы (7), заряд конденсатора равен сумме двух экспонент, убывающих с разными постоянными времени:                                                                  (20)

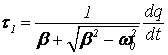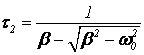                         ,                (21)

Процесс разрядки является апериодическим. Конкретный вид кривой разряда определяется начальными условиями. Два примера изображены на рис. 3.

в) β = ω_о. Оба корня р_1,2 уравнения (6) совпадают:    и решение (7) не является общим. Общее решение уравнения (5) имеет в этом случае вид:                          ,                                                                                       (22)

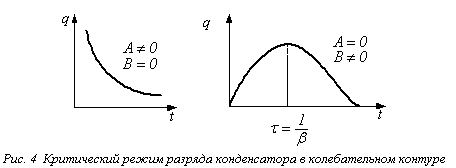
где константы А и В определяются из начальных условий. Этот режим является также апериодическим и носит название критического. Критический режим возникает при активном сопротивлении контура, равном критическому:

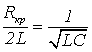                                                        ,                                      (23)

Два примера кривых разряда в этом случае изображены на рис. 4.

2. Для характеристики колебательной системы используется величина, называемая логарифмическим декрементом затухания. Логарифмический декремент затухания λ определяется как логарифм отношения двух последовательных значений амплитуды колебаний (рис.2):

                                                          (24)

Логарифмический декремент затухания связан с параметрами контура:

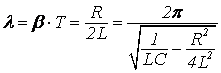                                                                     (25)

Для слабого затухания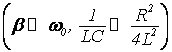        

                                                                                         (26)

За время τ, в течение которого амплитуда колебаний уменьшается в е раз, фаза колебания изменяется на величину   .

Так как одно колебание соответствует изменению фазы на 2π, то за время τ система совершает    колебаний. Отсюда получаем еще одно определение логарифмического декремента затухания:                        (27)

Важной характеристикой колебательной системы является добротность, определяемая выражением:                                                                   (28)