Исследование затухающих колебаний в колебательном контуре (лабораторная работа), страница 3

Общее решение уравнения (5):    ,                  (7)

где С₁ и С₂ - константы, определяемые из начальных условий. В зависимости от соотношений между β и ω различают несколько случаев:

а) β < ω_о, то  . Корни характеристического уравнения (6) в этом случае комплексны. Введем обозначение                                    (8)

Тогда   (i - мнимая единица, i² = -1) и решение уравнения (7) записывается в виде  

                или    ,

                        или    .           (9)

Амплитуда колебаний В(t) экспоненциально убывает со временем.

Таким образом, случай β < ω_о соответствует затухающим колебаниям (рис. 2).

Коэффициент затухания 

имеет, как видно из уравнений 9, 10, 11, следующий смысл:

величина численно равна времени, за которое амплитуда колебаний уменьшается в е раз (постоянная времени затухания).

Напряжение на обкладках конденсатора будет изменяться по аналогичному закону:

                                                             (10)

Сила тока в контуре:  

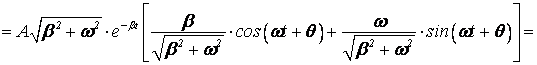
,                                                                    (11)

т.е. сила тока в контуре отстает по фазе от напряжения на обкладках конденсатора на величину φ, определяемую соотношениями

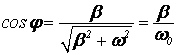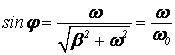                         ,                 (12)

Сдвиг фаз меняется в пределах от    до  .

Неизвестные константы: начальная амплитуда А и начальная фаза θ определяются из начальных условий. Пусть конденсатор был заряжен до напряжения U_o, а начальная сила тока в контуре была I_o. Тогда

                                ,             (13)

                                ,                           (14)

Период затухающих колебаний определяется как время, за которое фаза колебания (ωt + θ) изменяется на величину, равную 2π, т.е   .

Циклическая частота затухающих колебаний определяется формулой (8), т.е.

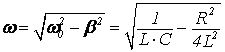                                          ,                   (15)

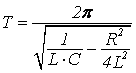                                                 ,                             (16)

т.е. свободные затухающие колебания происходят на частоте меньшей собственной.

Если потери в контуре отсутствуют (R=0), то колебания в контуре будут незатухающими:

                                 ,       .                   (17)