Функции покупательского спроса

5.3. Функции покупательского спроса

Связь модели поведения потребителей и функции спроса. Пусть в модели (5.6) цены и доход рассматриваются как меняющиеся параметры (для удобства переменную дохода будем обозначать в дальнейшем Z). Тогда решением параметрической оптимизационной задачи (5.6) будет вектор-функция Y* = Y*(P, Z). Она может быть выведена аналитически либо путем статистического обобщения оптимальных решений при различных значениях Р и Z. Компонентами вектор-функции Y* (P, Z) являются функции покупательского спроса на определенный товар от цен и дохода: .

Рассмотрим частный случай, когда изменяется только доход, а вектор цен остается неизменным (Р = Р°). Рис. 5.5 показывает: при увеличении дохода бюджетная линия перемещается параллельно самой себе и точками оптимума — спроса потребителей — будут точки M₁, М₂, М₃ (при нулевом доходе спрос на оба товара будет нулевым). Кривая, соединяющая точки О, M₁, М₂, является отображением вектор-функции покупательского спроса от дохода при заданном векторе цен.

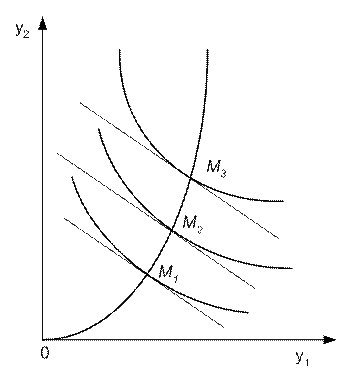
Рис. 5.5. Изменение спроса при росте доходов

Приведем простой пример построения функций спроса от дохода. Допустим, для двух товаров . Тогда . Необходимые условия оптимума дают систему уравнений: .

В результате подстановки первого уравнения во второе получаем . Подставим сюда выражение y₁ из третьего уравнения: , откуда . В результате получаем две функции спроса от дохода:

Между целевой функцией потребления и функциями покупательского спроса существует взаимная связь. Выше было показано, что функция спроса выводится из целевой функции потребления. Доказывается также, что из вектор-функции спроса, удовлетворяющей ряду естественных допущений, может быть выведена ЦФП. Нелогично поэтому признавать возможность и целесообразность построения и применения функций спроса и одновременно отрицать понятие "целевая функция потребления", а также все теоретические выводы, вытекающие из ее существования[1] .

Анализ влияния на покупательский спрос изменения цен и доходов удобно проводить на основе необходимых условий оптимума модели (5.6).

Если дифференцировать равенства (5.8) и равенство PY* = D по доходу и ценам, то будем получать системы из (n + 1) уравнений для частных производных  и ;  и . Например, дифференцирование бюджетного равенства по доходу и цене р_k дает уравнения:

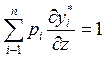 и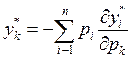

Знаки частных производных  и  характеризуют важные свойства товаров как объектов покупательского спроса. Для большинства товаров > 0 и < 0. Исключение составляют "малоценные" товары, спрос на которые при увеличении дохода снижается (среди продуктов питания это — хлеб, картофель, низкокачественные жиры и т.п., среди промышленных товаров — обувь и одежда устаревших моделей и фасонов и т.п.). В свою очередь среди товаров с  < 0 могут встречаться и такие товары[2], которые имеют > 0.

Функции спроса являются однородными нулевой степени относительно всех цен и дохода:  при . Действительно, пропорциональное изменение цен и дохода не влияет ни на положение бюджетного ограничения (определяющего область выбора потребителей), ни на целевую функцию. Покупательская способность (реальный доход) и соотношения цен остаются неизменными, меняется только масштаб цен.

В соответствии с формулой Эйлера для однородных функций имеем 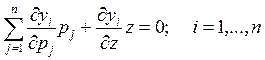. Разделив почленно обе части равенства на .у_i, получим

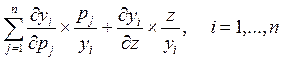                                 (5.14)

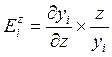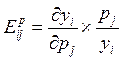Выражение  есть коэффициент эластичности спроса на товар i от дохода, характеризующий относительное изменение спроса по отношению к относительному изменению дохода. Выражение  есть коэффициент эластичности спроса на товар i от цены на товар j, характеризующий относительное изменение спроса по отношению к относительному изменению цены. Из (5.14) следует

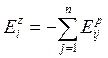                          (5.15)

Если , то , откуда 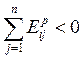 (т.е. хотя бы один коэффициент эластичности от цены должен быть отрицательным). Если же 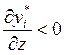 (малоценный товар), то  и 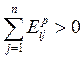 (т.е. хотя бы один коэффициент эластичности от цены должен быть положительным).

Построение общих функций спроса  для всей совокупности товаров требует очень значительных объемов информации и по трудоемкости сопоставимо с построением ЦФП по эмпирическим данным. Поэтому в экономическом анализе и прогнозировании чаще используются частные функции покупательского спроса для отдельных групп товаров, которые характеризуют изменение спроса либо только от дохода, либо только от цен, либо от дохода и цен на те же выделенные товары.

Функции и коэффициенты эластичности спроса от дохода. На практике функции покупательского спроса строятся и применяются главным образом для отдельных групп товаров. При этом выбираются такие типы функций, которые отражают устойчивые тенденции (эмпирические закономерности) изменения спроса и потребления при увеличении дохода.

В конце XIX в. немецкий статистик Э. Энгель сформулировал эмпирические законы потребления и построил кривые, в соответствии с которыми с ростом дохода доля расхода на питание уменьшается, доля расхода на одежду и жилье остается стабильной и т.п. (функции спроса от дохода часто поэтому называют кривыми Энгеля). Этот же принцип разграничения групп товаров по типам функций спроса (потребления) от дохода использовал шведский экономист Л. Торнквист. Он предложил специальные виды функций (функции Торнквиста) для трех укрупненных групп товаров: первой необходимости (I), второй необходимости (II), предметов роскоши (III). Графики этих функций проводятся на рис. 5.6.

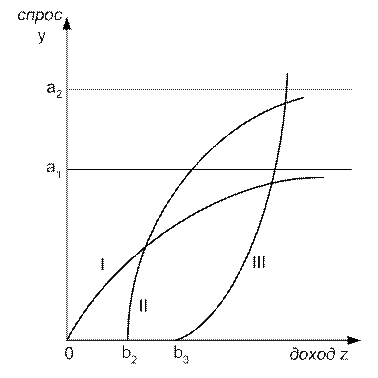
Рис. 5.6. Функции спроса от дохода (кривые Торнквиста)

Функция для предметов первой необходимости имеет вид

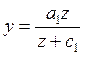        (5.16)

Она отражает тот факт, что рост спроса (потребления) на многие товары, удовлетворяющие самые насущные потребности, постепенно замедляется (так что 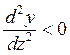) и имеет предел a₁ (кривая асимптотически приближается к линии a₁).

Функция спроса на предметы второй необходимости имеет вид

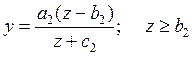                     (5.17)

Эта функция также имеет предел (a₂), но более высокого уровня. Спрос на эту группу товаров появляется только после того, как доход достигает величины b₂.

Наконец, функция спроса на предметы роскоши выражается формулой