Экономика и менеджмент \ Экономика природопользования

Увеличение потребности и рентные оценки месторождений. Сущность несущей способности экосистемы. Задача по таблице средних индивидуальных затрат, страница 3

Общая потребность составляет 900, эту потребность можно удовлетворить с помощью добычи на 4-м и 5-м месторождениях.

А) Определить оценки запасов 1, 4 и 7-го месторождений.

;  ; 

Б) Определить сроки отработки месторождений:

; ; ; ; ; .

Вариант №3

1. Доказать, что горную ренту нельзя интерпретировать категориями дифференциальной земельной ренты.


Земельная рента

Когда речь идет об использовании земли, мы имеем дело с ресурсом бесконечным по времени использования запас земли не уменьшается во времени и не зависит от использования в предыдущие годы (может изменяться только продуктивность земли, но это уже переменная другой категории)

 - урожайность участка,

Сбоку подписаны двойственные переменные
 
Задача:

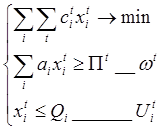
Рента определяется как

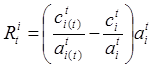
 – индекс самого «плохого» (затратного) месторождения, тогда

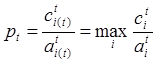
, т.е.    (*)

Двойственная задача:

     (**)

Сопоставляя (*) и (**), получим

 и

Горная рента

Когда речь идее о добычи природных ресурсов, типа полезных ископаемых, ключевым моментом является то, что их запас ограничен и уменьшается после каждого периода использования, т.е. доступное количество к году t

Задача:

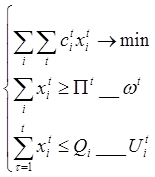
Рента определяется как

 – индекс самого «плохого» (затратного) месторождения, тогда

Двойственная задача:

       (*)

В том числе это выполнено для худшего месторождения:

    (**)

Из (*) и (**)


Видим, рассматривая земельные ресурсы и полезные ископаемые, мы получили совершенно разные рентные оценки, это вызвано описанными в начале особенностями этих природных ресурсов.

2. Влияние транспортного фактора на оптимальную оценку природных ресурсов.

Введем в модель транспортный фактор. Используется модель подробно описанная в 1-м вопросе варианта №1.

Пусть, как и ранее, мы имеем n пунктов добычи некоторого природного ресурса , только теперь введем m пунктов потребления . Помимо текущих и капитальных затрат на добычу, существуют затраты на доставку ресурса потребителям.

Пусть

 – объем перевозок ресурса от i-го источника до j-го потребителя;

Записав к данной задаче двойственную можно найти средние индивидуальные затраты:

Видим, что по сравнению с основной моделью (не учитывающей транспортный фактор) средние индивидуальные затраты стали привязаны не к пункту производства, а к паре: пункт потребления – пункт производства.

Кроме того, в числителе добавилось слагаемое, отражающее транспортные затраты.
 
– удельные транспортные затраты на перевозку ресурса от i-го источника до j-го потребителя;

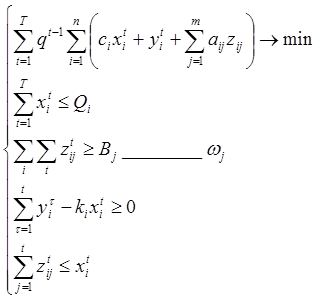
 – предельные затраты, двойственная оценка второго ограничения.

Введение в анализ транспортных затрат может существенно изменить ситуацию и повлиять на выбор месторождений для разработки. Месторождение с низкими текущими и капитальными затратами, которые являлись наименее затратными до учета транспортного фактора, после этого могут не войти в оптимальный план разработки.

3.  Частные чистые выгоды описываются функцией: 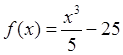, а внешние издержки . Определить налог Пигу.

При определении оптимального уровня экономической активности пользуемся условием равенства предельных частных чистых выгод предельным внешним издержкам, т.е.

   – оптимальный уровень экономической активности.

Налог Пигу:

4.  Задача по таблице средних индивидуальных затрат .

Вначале определяем минимальные  для каждого месторождения i:

; ; ;;

Упорядочиваем их по возрастанию (внизу подпишем доступный объем добычи):

  200     350      400       150     300               запасы на месторождениях

  200     550      950                                   запасы накопительным итогом

Общая потребность составляет 700, эту потребность можно удовлетворить с помощью добычи на 1-м, 4-м и 5-м месторождениях. Сроки начала разработки соответственно 4-ый 3-ий  и 4-ый периоды.

Вариант №4

Скачать файл