Градуировка спектроскопа. Определение длин волн излучения ртутной лампы (лабораторная работа), страница 8

При очень больших, но близких по значению n_i и n_f можно сделать следующие подстановки:

,      ,      .

В таком случае для частоты фотона принимает следующий вид:

.

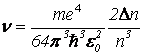При  это уравнение совпадает с классическим уравнением для частоты обращения электрона (21). Для  мы получаем гармоники основной частоты.

Таким образом, применение модели Бора (призванной объяснить явления микромира) к задачам макромира приводит к результатам, которые идентичны результатам, полученным классическими методами. В этом и заключается основной философский смысл принципа соответствия

ВЫПОЛНЕНИЕ  РАБОТЫ

1. Включите неоновую лампу и поставьте ее непосредственно перед щелью спектроскопа так, чтобы светящийся промежуток неоновой лампы был на уровне щели.

2. Посмотрите в окуляр прибора и найдите в спектре следующие линии:

Таблица 1

Цвет линии	Соответствующая ей длина волны (мм)
Ярко-красная	640,2
Красно-оранжевая	615,3
Желтая	585,2
Светло-зеленая (первая справа)	576,0
Зеленая (правая)	540,0
Зеленая (левая)	533,0
Сине-зеленая	484,0

3. Вращая винт спектроскопа установите вертикальную метку окуляра у правой границы ярко-красной линии, определите показания прибора и занесите их в таблицу 2.

4. Подведите метку к левой границе ярко-красной линии и занесите показания прибора в таблицу 2.

5. Пункты 3 и 4 повторить со всеми линиями неоновой лампы.

6. Выключите неоновую лампу и включите ртутную.

7. Поместите щель спектроскопа против окна ртутной лампы.

8. Повторите пункты 3 и 4 со всеми четко различимыми линиями ртутной лампы.

9. Занесите результаты показаний прибора для неоновой лампы в табл. 2.

10. Определите для всех длин волн  по формуле

11. Постройте график зависимости  для неоновой лампы.

12. Методом интерполяции найдите неизвестные длины волн ртутной лампы и занесите в табл. 2.

№ п/п	Цвет линии	Длина волны (нм)	хлев.	хправ	<x>