Градуировка спектроскопа. Определение длин волн излучения ртутной лампы (лабораторная работа), страница 6

                                                      .

Тогда кинетическая энергия электрона, определяемая соотношением (3), будет равна:

.

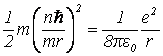Откуда можно найти радиус «незлучающих» орбит:

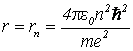                                     ,           .               (11)

Для основного состояния  так называемый боровский радиус будет равен:

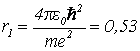                                               Å.                                 (12)

Этот результат совпадает со значением, полученным при определении радиуса атома из уравнения (5) для планетарной модели.

Из уравнения (11) видно, что       ,                                          (13)

т.е. радиусы орбит для стационарных состояний также квантованы и равны соответственной  . Каждый из этих радиусов пропорционален квадрату целого числа n, называемого главным квантовым числом.

Заменив r в уравнении (5) выражением (11), получим:

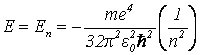                                       ,                               (14)

где знак «минус» означает, что система является связанной. Таким образом, можно сделать вывод о том, что энергия атома квантована. Разрешенные значения энергии определяются уравнением (14), когда n принимает значения  . Подстановка значений массы и заряда электрона ,  в уравнение (14) дает:

                                                  эВ,    .                       (15)

Состояние с минимальной энергией, или основное состояние, соответствует , а его энергия  эВ.

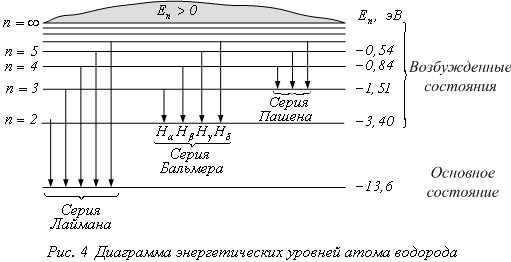
На рис. 5 приведена диаграмма энергетических уровней, на которой горизонтальными кривыми отмечены разрешенные значения для атома водорода. Заметим, что все состояния от  до  являются связанными, так как имеют отрицательные энергии. При увеличении n и приближении к  энергетические состояния сближаются все больше и больше до тех пор, пока разница в энергиях между двумя последовательными состояниями не станет настолько малой, что распределение энергетических уровней практически превратится в непрерывный спектр. Это хорошо согласуется с классической планетарной моделью и принципом соответствия. Выше места слияния уровней, где , энергетические состояния обладают положительной энергией (Е > 0). При этом система является несвязанной, т.е. электрон становится свободным.

Из уравнения (14) видно, что если атом находится в основном состоянии, то для удаления электрона из атома требуется энергия 13,6 эВ. Следовательно, энергия связи (Е_св) и энергия ионизации (Е_ион) для атома водорода, находящегося в основном состоянии, равны и  эВ.

Этот постулат (проверенный экспериментально) был использован нами в уравнении (5) для планетарной модели атома при расчете боровского радиуса Å.