16.3. Общая модель экономического взаимодействия подсистем
Модель и ее основные свойства. Пусть в народном хозяйстве выделяются т
подсистем нижнего уровня (k = 1, ..., m) и одна подсистема
верхнего уровня с номером т + 1 – центральная подсистема. Будем
предполагать, что подсистемы могут обмениваться результатами своей
деятельности. Интенсивность такого обмена для подсистемы kбудем характеризовать
вектором ![]() – сальдо обмена. Тогда каждый план
– сальдо обмена. Тогда каждый план ![]() подсистемы k естественно представлять
в виде
подсистемы k естественно представлять
в виде
![]() (16.3)
(16.3)
где вектор ![]() описывает интенсивность различных видов
внутренней деятельности подсистемы;
описывает интенсивность различных видов
внутренней деятельности подсистемы; ![]() – множество
допустимых планов k-й подсистемы. Цели развития каждой подсистемы
выражаются в виде функции
– множество
допустимых планов k-й подсистемы. Цели развития каждой подсистемы
выражаются в виде функции ![]() , зависящей лишь
от выбранных вариантов интенсивности внутренней деятельности – векторов
, зависящей лишь
от выбранных вариантов интенсивности внутренней деятельности – векторов ![]() . Будем предполагать также, что
условие
. Будем предполагать также, что
условие ![]() допустимости общего решения всей системы
можно представлять как условие сбалансированности обмена результатами
деятельности
допустимости общего решения всей системы
можно представлять как условие сбалансированности обмена результатами
деятельности
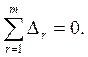 (16.4)
(16.4)
С рассматриваемой системой может быть сопоставлена кооперативная
игра с характеристической функцией следующего типа: пусть X– композиция возможных
планов подсистем ![]() , таких, что выполняется условие
, таких, что выполняется условие ![]() Тогда
Тогда ![]() в том и
только в том случае, когда
в том и
только в том случае, когда ![]() (здесь, как и выше,
(здесь, как и выше, ![]() – произвольная коалиция подсистем, а
– произвольная коалиция подсистем, а ![]() – множество значений целевых функций
участников).
– множество значений целевых функций
участников).
Следующее утверждение дает условия непустоты ядра для рассматриваемого класса моделей взаимодействия[1].
Утверждение 1. Предположим, что множества ![]() непустые, выпуклые, замкнутые,
ограниченные, а функции
непустые, выпуклые, замкнутые,
ограниченные, а функции ![]() вогнутые, непрерывные (k= 1, ..., т). Пусть
также каждое множество
вогнутые, непрерывные (k= 1, ..., т). Пусть
также каждое множество ![]() содержит вектор (xk, 0)[2]. Тогда ядро рассматриваемой игры
непусто.
содержит вектор (xk, 0)[2]. Тогда ядро рассматриваемой игры
непусто.
Перейдем теперь к описанию некооперативной игры, соответствующей
рассматриваемой системе, и условий существования равновесных решений. Будем
предполагать, что управляющим параметром центральной подсистемы является вектор
цен р. В качестве множества возможных векторов цен Qрассмотрим совокупность
всех неотрицательных векторов соответствующей размерности, все компоненты
которых в сумме равны 1. Будем считать, что множество ![]() состоит
из подмножеств всех возможных векторов, удовлетворяющих (при данном р) условию
финансовых балансов внешних связей следующего типа:
состоит
из подмножеств всех возможных векторов, удовлетворяющих (при данном р) условию
финансовых балансов внешних связей следующего типа:
![]() (16.5)
(16.5)
Для спецификации некооперативной игры (т + 1) лиц с
зависимыми множествами стратегий остается определить задачу подсистемы верхнего
уровня – (т + 1)-го участника. Предположим, что он решает следующую
задачу: для каждого набора ![]() планов подсистем найти
вектор цен
планов подсистем найти
вектор цен ![]() , минимизирующий в стоимостном выражении
общее сальдо обмена, т.е.
, минимизирующий в стоимостном выражении
общее сальдо обмена, т.е.
![]() ;
;
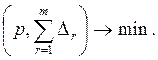
Исследуем теперь связь между равновесными состояниями данной модели взаимодействия и решениями по Нэшу соответствующей игры (т + 1) лиц.
Утверждение 2. Пусть ![]() – состояние
равновесия. Тогда пара
– состояние
равновесия. Тогда пара ![]() является точкой Нэша соответствующей
игры.
является точкой Нэша соответствующей
игры.
Действительно, векторы ![]() являются решениями
задачи k-й подсистемы (k = 1, ..., m) при векторе цен р*. Далее, вектор р* является решением задачи подсистемы m + 1, так как
являются решениями
задачи k-й подсистемы (k = 1, ..., m) при векторе цен р*. Далее, вектор р* является решением задачи подсистемы m + 1, так как 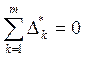 . Обратное утверждение, вообще говоря,
неверно, однако имеет место.
. Обратное утверждение, вообще говоря,
неверно, однако имеет место.
Утверждение 3. Пусть (р*, X*) – точка Нэша. Тогда
определяемые ею решения подсистем нижнего уровня непротиворечивы, т.е. 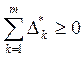 , где
, где ![]() – планы
по обмену продукцией, соответствующие равновесным решениям, составляющим вектор
X*.
– планы
по обмену продукцией, соответствующие равновесным решениям, составляющим вектор
X*.
Утверждение 4. Пусть (р*, X*) – точка Нэша и выполнены следующие предположения:
1) для данного р*и каждого k (k = 1, ..., т) ограничение
(16.3) выполняется как равенство для соответствующих вектору X*планов по обмену продукцией ![]() , k = 1,...,т, т.е.
, k = 1,...,т, т.е. ![]() ;
;
2) продукты желательны в том
смысле, что, если цена продукта равна нулю, сальдо обмена по этому продукту,
вычисленное в соответствии с любыми оптимальными при данном векторе цен
решениями подсистем, является отрицательным, т.е. если ![]() рi= 0, то
рi= 0, то 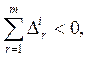 , где
, где ![]() ,
обозначает компоненту с номером iвектора
,
обозначает компоненту с номером iвектора ![]() . Тогда (р*, X*) – состояние
равновесия.
. Тогда (р*, X*) – состояние
равновесия.
Данное утверждение позволяет установить теорему существования состояния (траектории) равновесия в рассматриваемой системе на основе следующего утверждения о существовании решения по Нэшу соответствующей ей игры (т + 1) лиц.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.