Общая модель экономического взаимодействия подсистем, страница 2

Утверждение 5. Предположим, что, как и в условиях утверждения 1, множества  являются выпуклыми, замкнутыми, а функции f_k – вогнутыми, непрерывными (k = 1,...,m). Предположим также, что для всякого k= 1,...,m множество  содержит вектор , такой, что  (т.е. каждая подсистема может произвести положительное количество каждого из обмениваемых продуктов). Тогда описанная выше игра имеет состояние равновесия.

Указанные условия обеспечивают выполнение условий теоремы о существовании точки Нэша игры (m + 1) лиц.

Соотношение ядра и равновесия. Связь двух подходов к исследованию рассматриваемой системы (кооперативного и некооперативного), а также эффективность равновесных решений подсистемы описывают следующее.

Утверждение 6. Предположим, что (р^*, X^*) – равновесное решение, а ограничение (16.5) во всех задачах подсистем при векторе цен р^*– существенно в том смысле, что  для всех планов по обмену продукцией, соответствующих векторам , полученным композицией множества оптимальных решений  задач подсистем.

Тогда X^*принадлежит ядру рассматриваемой системы (см. ВСМ, с. 120).

Обратное утверждение, вообще говоря, неверно, так что ядро (когда не пусто) содержит кроме равновесных согласованных планов (когда таковые существуют) и другие согласованные планы.

Математическое исследование связи между ядром и равновесием приводит к выводу, что "различия" между ними проистекают в основном из-за малого числа взаимодействующих подсистем и что при увеличении числа подсистем эти различия имеют тенденцию убывать[3].

Нечеткие коалиции и нечеткое ядро. Формально нечеткой коалицией называется любой набор  неотрицательных чисел – "долей" участия подсистем в данной коалиции. При этом говорят, что такая коалиция блокирует , если существуют возможные варианты функционирования подсистем , такие, что

;

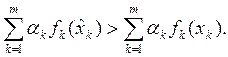
В частности, если  для всех  и  для , то приходим к старому понятию блокирования по коалиции S.

Нечетким ядром называется множество векторов , не блокируемых никакими нечеткими коалициями.

При естественных предположениях устанавливается эквивалентность нечеткого ядра и множества равновесных решений и тем самым – двух теоретических подходов: кооперативного и некооперативного. Таким образом, равновесные решения в определенном смысле удовлетворяют наиболее жестким требованиям к оптимальности в многоцелевой системе и никакие другие решения этим требованиям не удовлетворяют.

Утверждение 7. Предположим, что для каждого k = 1,...,m функция f_k(x_k) является вогнутой, непрерывной, а множества  – выпуклым компактом. Пусть  – точка нечеткого ядра. Предположим также, что для всякого k = 1, ..., m существуют  и , такие, что  и . Тогда найдется вектор р^*, такой, что состояние (р^*, X^*) является равновесием (схему доказательства см. в ВСМ, с. 124 – 125).

Свойства модели взаимодействия с . Выше предполагалось, что для каждой подсистемы выполняется условие .

Утверждение 8. Будем считать, что выполнены все предположения утверждения 7, за исключением условия, что X^*принадлежит нечеткому ядру. Пусть вместо этого X^*– эффективная точка множества . Тогда существуют числа , такие, что

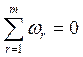                                                                (16.6)

и (р^*,X^*) является равновесием в модифицированной модели экономического взаимодействия, полученной заменой условия (16.3) финансовых балансов внешних связей каждой подсистемы на соотношения:

                                                                                                       (16.7)

Далее, при априорно заданных величинах сальдо внешних связей  равновесное решение в указанной модифицированной модели экономического взаимодействия определяет оптимум по Парето в условиях, аналогичных предположениям утверждения 6, т.е. имеет место следующее утверждение.

Утверждение 9. Предположим, что (р^*, X^*) является равновесным решением модифицированной модели экономического взаимодействия с априорно заданными величинами сальдо внешних связей . Предположим также, что ограничения (16.7) в соответствующих задачах подсистем (при векторе цен р^*) являются существенными. Тогда X^*является оптимальной по Парето точкой множества .