





6.3. Математический анализ модели межотраслевого баланса
Свойства матрицы А. Матрица коэффициентов прямых материальных затрат А относится к хорошо изученному в математике классу неотрицательных матриц (подробнее см. [2. Ч. I. Гл. 1]). Но коэффициенты матрицы А не могут принимать произвольные положительные значения. Очевидно, что все диагональные элементы матрицы А должны быть меньше единицы. В противном случае производство лишается всякого смысла (если аii> 1, то xii > xi). Существуют и другие менее очевидные ограничения значений коэффициентов аii, выражающие требования общественного производственного процесса.
В частности, произведения
коэффициентов, симметричных относительно главной
диагонали, должны быть, по крайней мере, меньше единицы: alkakl< 1. Для того чтобы пояснить необходимость
этого условия, рассмотрим следующий пример. Пусть производственная система
изготовляет два продукта: уголь и металл. При этом на производство 1 т металла расходуется 2 т угля,
на 1 т угля - 1 т металла (а12 а21=2). При таких
коэффициентах затрат производство превращается в особый способ уничтожения ресурсов, так как для
изготовления металла в конечном
счете требуется еще большее количество металла, а для добычи угля – еще большее количество угля. "Производство" не
только не может дать конечной продукции, а
непрерывно должно субсидироваться извне ресурсами угля и металла.
Коэффициенты матрицы 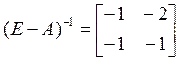 отрицательны, что также противоречит соотношениям "нормальной" экономики.
отрицательны, что также противоречит соотношениям "нормальной" экономики.
Особенности матриц в ценностном и натуральном
выражении. Указанные выше ограничения
на значения отдельных коэффициентов не зависят от применяемых единиц измерения,
так как в соответствии с (6.15) ![]() . Однако в общем случае выбор единиц измерения
существенно влияет на анализ свойств матриц межотраслевого баланса. Для матриц
межотраслевого баланса в ценностном выражении обычно выполняются условия
. Однако в общем случае выбор единиц измерения
существенно влияет на анализ свойств матриц межотраслевого баланса. Для матриц
межотраслевого баланса в ценностном выражении обычно выполняются условия ![]() (см.,
например, последнюю строку табл. 6.2). Если же для некоторой k-й отрасли
(см.,
например, последнюю строку табл. 6.2). Если же для некоторой k-й отрасли
![]() , то экономически это означает, что данная отрасль
настолько убыточна, что ее убытки перекрывают расходы на амортизацию и оплату
труда. Очевидно, что в условиях хозрасчета такое состояние отрасли совершенно
неприемлемо.
, то экономически это означает, что данная отрасль
настолько убыточна, что ее убытки перекрывают расходы на амортизацию и оплату
труда. Очевидно, что в условиях хозрасчета такое состояние отрасли совершенно
неприемлемо.
Из линейной алгебры известно, что одна из норм матрицы
A определяется как ![]() .
Следовательно,
.
Следовательно, ![]() , когда
, когда ![]() .
Например, для приведенной выше матрицы межотраслевого баланса СССР
.
Например, для приведенной выше матрицы межотраслевого баланса СССР ![]() .
.
Из того, что ![]() ,
вытекает ряд следствий, важных для экономического анализа:
,
вытекает ряд следствий, важных для экономического анализа:
1) ![]() ;
;
2) ![]() (6.25)
(6.25)
3) ![]()
4) все собственные значения λi матрицы А по модулю меньше единицы, а наибольшее собственное значение положительно (теорема Фробениуса—Перрона)[1];
5) все главные миноры матрицы (Е - А) положительны и меньше единицы.
В матрицах межотраслевого баланса в натуральном
выражении условия ![]() практически
никогда не выполняются. Более того, многие коэффициенты этих матриц больше
единицы. Однако можно попытаться подобрать такие новые измерители (матрицу Р),
что для подобной матрицы
практически
никогда не выполняются. Более того, многие коэффициенты этих матриц больше
единицы. Однако можно попытаться подобрать такие новые измерители (матрицу Р),
что для подобной матрицы ![]() будет выполняться условие
будет выполняться условие ![]() и
следствия (6.25). Из линейной алгебры известно, что подобные матрицы имеют равные по величине собственные
значения и главные миноры (матрицы
(Е - А) и
и
следствия (6.25). Из линейной алгебры известно, что подобные матрицы имеют равные по величине собственные
значения и главные миноры (матрицы
(Е - А) и ![]() также являются
подобными, так как
также являются
подобными, так как ![]() .
.
Понятие о разложимых и неразложимых матрицах. В теории матриц разложимыми называются такие матрицы А, которые одновременной перестановкой строк и столбцов приводятся к виду
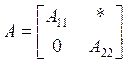 (6.26)
(6.26)
![]() ,
, ![]() —
квадратные блоки, включающие ненулевые элемент; 0 - блок, состоящий только из нулей; * — блок, элементы которого могут принимать любые значения.
—
квадратные блоки, включающие ненулевые элемент; 0 - блок, состоящий только из нулей; * — блок, элементы которого могут принимать любые значения.
Матрица А неразложима, если для нее не существует таких одновременных перестановок строк и столбцов, которые приводили бы ее к разложимой форме (даже несмотря на наличие большого числа нулевых элементов). Если матрица А неразложима, то каждая отрасль непосредственно или косвенно использует продукцию всех других отраслей, а ее продукция непосредственно или косвенно расходуется при производстве продукции всех других отраслей, т.е. все пары отраслей находятся в двусторонней связи (подробнее о свойствах неразложимых матриц и об использовании этих свойств в экономическом анализе и плановых расчетах см. [1.С. 194 — 214]).
Продуктивность матрицы А. Введенное в гл. 2 общее понятие продуктивности экономической системы в модели межотраслевого баланса связывается исключительно со свойствами матрицы А. Продуктивной экономической системе соответствует такая матрица коэффициентов А, которая обеспечивает возможность получения конечной продукции (вектора Y) при соответствующих пропорциях развития производства векторе X).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.