принятыми стандартами качества окружающей среды, однако они могут устанавливаться также и исходя из реальных технико-экономических возможностей. Деятельность по уничтожению загрязнителей имеет смысл (т.е. соответствующие xi> 0), если Y2 ≤А21Х1 + А22Х2. Поэтому для общности вместо матричного равенства можно записать Х2 ≥A21X1+A22X2-Y2.
Матрица
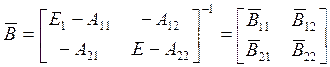
является обобщением матрицы коэффициентов полных
затрат продукции. Элементы, входящие в блоки этой матрицы, имеют следующее
экономическое содержание: ![]() - коэффициенты полных
затрат производимой продукции на единицу конечной продукции,
- коэффициенты полных
затрат производимой продукции на единицу конечной продукции, ![]() — коэффициенты полных затрат продукции на
единицу уменьшения неуничтоженных загрязнителей,
— коэффициенты полных затрат продукции на
единицу уменьшения неуничтоженных загрязнителей, ![]() —
коэффициенты необходимого уничтожения загрязнителей на единицу конечной
продукции;
—
коэффициенты необходимого уничтожения загрязнителей на единицу конечной
продукции; ![]() — коэффициенты необходимого уничтожения
загрязнителей на единицу уменьшения неуничтоженных загрязнителей.
— коэффициенты необходимого уничтожения
загрязнителей на единицу уменьшения неуничтоженных загрязнителей.
Соотношение ![]() ≥ 0 является необходимым условием функционирования расширенной системы
межотраслевых связей. Его выполнимость во многом зависит от эффективности (технологичности) включаемых в систему видов деятельности по
уничтожению загрязнителей. Имеющиеся
способы уничтожения некоторых загрязнителей требуют столь высоких материальных затрат, что
добавление к матрице
≥ 0 является необходимым условием функционирования расширенной системы
межотраслевых связей. Его выполнимость во многом зависит от эффективности (технологичности) включаемых в систему видов деятельности по
уничтожению загрязнителей. Имеющиеся
способы уничтожения некоторых загрязнителей требуют столь высоких материальных затрат, что
добавление к матрице ![]() соответствующих строк и столбцов может приводить к тому,
что в матрице
соответствующих строк и столбцов может приводить к тому,
что в матрице ![]() будут
появляться отрицательные коэффициенты.
будут
появляться отрицательные коэффициенты.
Пусть условие ![]() ≥0 выполняется, вектор Y1, фиксирован, а
вектор
≥0 выполняется, вектор Y1, фиксирован, а
вектор ![]() показывает допустимые размеры неуничтожаемых
загрязнителей (например, на уровне прошлого года). Тогда
показывает допустимые размеры неуничтожаемых
загрязнителей (например, на уровне прошлого года). Тогда
![]() ,
, ![]()
Повышение требований к качеству окружающей среды выражается в том, что
новый вектор Y2 будет иметь меньшие значения компонент, чем вектор ![]() , т.е. Y2 =
, т.е. Y2 = ![]() —ΔY2, ΔY2> 0. При ΔY=
—ΔY2, ΔY2> 0. При ΔY= ![]() достигается полная очистка.
достигается полная очистка.
Более строгие требования к очистке ведут к увеличению объемов производства (по
сравнению с ![]() и
и ![]() ): ΔX1 =
): ΔX1 = ![]() >0, ΔX2 =
>0, ΔX2 = ![]() > 0. Максимальные приросты производства
> 0. Максимальные приросты производства ![]() и
и ![]() получаются при
полной очистке:
получаются при
полной очистке: ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
Система (7.16) может быть использована также для решения задачи со смешанным составом неизвестных. Например, надо найти Х1 и Y2 при заданных Y1и Х2. Дня этого вначале решается система Х1= (E1 – A11)-1 (A12X2+ Y1), а затем находится вектор неуничтоженных загрязнителей: Y2=A21 Х1 -(E2 – A22) Х2/
Главные трудности в использовании рассматриваемой модели состоят в подготовке надежной информации для блоков A12, A21, A22 В последние годы здесь наметились позитивные изменения, связанные с общим расширением информационного обеспечения эколого-экономических исследований и практической деятельности по охране окружающей среды. Относительно проще определить коэффициенты блока A21. Это позволяет использовать исходную модель в следующем сокращенном варианте:
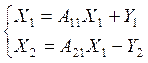 (7.18)
(7.18)
В этой системе выпуск и уничтожение загрязнителей не оказывают влияния на производство традиционных видов продукции и их конечное использование. В то же время система (7.17) позволяет учитывать влияние материального производства
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.