Экономика и менеджмент \ Экономика

Математический анализ модели межотраслевого баланса, страница 3

Количественное выражение коэффициентов косвенных и полных затрат может быть получено из анализа схемы.

Косвенные затраты первого цикла - это прямые затраты на производство того количества средств производства, которое потребляется при изготовлении единицы продукции. Они определяются следующим образом:

,

Косвенные затраты второго цикла выражаются уже более сложным образом. Суммируются элементы косвенных затрат второго цикла по первым индексам, и каждый элемент является произведением трех коэффициентов прямых затрат.

Например, в . Если продолжим цепи взаимосвязей, то получим косвенные затраты третьего, четвертого цикла и т.д. Последовательно учитывая косвенные затраты все более высокого цикла, т.е. дальше отстоящего от данного процесса производства, в пределе должны получить коэффициенты полных затрат. Однако поэлементные вычисления становятся все более громоздкими. И осуществлять их становится практически невозможно, если не прибегнуть к обобщению расчетов в виде математических формул.

Коэффициенты косвенных затрат первого цикла имеют наиболее простую структуру: они слагаются из произведений коэффициентов прямых затрат. При определении косвенных затрат второго цикла соответствующие коэффициенты прямых затрат умножаются на отдельные слагаемые косвенных затрат первого цикла. Если предварительно суммировать слагаемые косвенных затрат первого цикла, то получим компактные формулы косвенных затрат второго цикла:

;

Используя метод индукции, можно показать, что общие формулы косвенных затрат для любого цикла имеют вид

                                                    (6.27)

                             (6.28)

где т — любое целое положительное число (при этом )/

Практические расчеты показывают, что с учетом косвенных затрат до третьего — пятого циклов для большинства видов продукции и ресурсов получается хорошее приближение к полным затратам.

Например (см. табл. 6.2 и 6.3), прямые затраты продукции тяжелой промышленности на 1000 руб. продукции легкой промышленности составляют 45,2 руб., а полные - 366,1 руб. (в 8,1 раза больше). Косвенные затраты первого цикла равны 95,2 руб., второго цикла - 83,4, третьего цикла — 57,8 ... пятого цикла - 21,2 руб. Сумма прямых и косвенных затрат до пятого цикла включительно составляет 92,6 % полных затрат.

Выведем общие формулы коэффициентов полных затрат. По определению полных материальных затрат как суммы прямых и всех косвенных затрат (при т →∞) имеем

(6.29)

Подставив в (6.29) выражения (6.27) для различных циклов, получим

Очевидно, что при т →∞ . В итоге получаем

(6.30)

Для определения коэффициентов полных материальных затрат на производство единицы продукции j требуется решить систему из п уравнений (6.30) с фиксированными j и i = 1, ..., п. Для определения всей матрицы коэффициентов полных затрат сij необходимо решить п таких систем уравнений.

Формула коэффициентов полных затрат ресурсов выводится аналогично

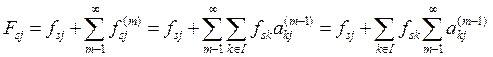
Таким образом

     (6.31)

По формуле (6.31) исчисляются полные затраты труда, основных фондов и других производственных ресурсов, а также коэффициенты полных затрат элементов условно-чистой продукции. После того как определены коэффициенты ckj, вычисление коэффициентов Fsjне представляет какой-либо трудности.

Экономическая сущность коэффициентов полных затрат может исследоваться также с иных позиций. Для этого можно рассмотреть процесс образования полных затрат определенного вида продукции (или ресурса) на производство всех видов продукции (см. [1. С. 146 — 150]). Такой подход приводит к следующим формулам коэффициентов полных затрат:

      (6.32)

    (6.33)

Соотношения матриц коэффициентов прямых, косвенных и полных затрат. Пусть а(m) — матрица коэффициентов косвенных материальных затрат цикла т; f(m) — матрица косвенных затрат ресурсов цикла т; С — матрица коэффициентов полных материальных затрат; F— матрица коэффициентов полных затрат ресурсов. Тогда формулы (6.27), (6.28), (6.30), (6.31) в матричном виде записываются так:

          (6.34)

          (6.35)

    (6.36)

(6.37)

В соответствии с (6.34) А1 =А∙А=А2,А(2) =А • A(l) = А3 и т.д. В общем же случае матрица косвенных материальных затрат цикла (m) равна (m + 1)-й степени матрицы А:

(6.38)

Из определения полных материальных затрат следует

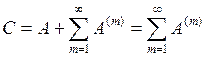                                              (6.39)

В линейной алгебре известно аналогичное разложение в степенной ряд: - (если А(т)→ 0 при т→∞). Очевидно, что если существует (Е - A)-1 и Am→0 (при m т→∞) то[3]

C = (E-A)-1 -E                                      (6.40)

Пользуясь матричными обозначениями, легко показать, что формулы (6.30) и (6.32), (6.31) и (6.33) тождественны (см. ММСЭ, с. 267).

Скачать файл