Математический анализ модели межотраслевого баланса, страница 2

Матрица А называется продуктивной, если существует неотрицательный вектор , позволяющий получить положительный вектор конечной продукции: (Е-А)Х =Y>0. Для неразложимых матриц определение продуктивности имеет более общий вид. Неразложимая матрица А продуктивна, если существует такой вектор , что .

Для отчетного межотраслевого баланса (в котором всегда ) свойство продуктивности проверяется очень просто. Если , то система продуктивна. Однако если некоторые , то из этого еще нельзя сделать вывод о непродуктивности матрицы А. Можно, взяв вместо неположительных компонент вектора Y положительные значения, рассчитать новые значения X. И если при этом окажется, что , то матрица А продуктивна.

Продуктивность матрицы Aможно определить и по отношению к модели межотраслевых зависимостей цен. Матрица Aпродуктивна, если существует такой вектор, что. Неразложимая матрица А продуктивна, если существует такой вектор, что.

Это означает, что можно подобрать цены, обеспечивающие получение неотрицательной чистой продукции во всех отраслях и хотя бы в некоторых отраслях положительной чистой продукции. Для отчетных межотраслевых балансов в ценностном выражении убедиться в том, что матрица А продуктивна, как правило, очень просто: достаточно, чтобы  и хотя бы для одного j было z_j > 0. Однако если эти условия не выполняются, то нельзя утверждать, что матрица А непродуктивна.

Для продуктивности матрицы А необходимо и достаточно, чтобы выполнялось одно из нижеследующих условий.

1. Все главные миноры матрицы (Е — А) положительный меньше единицы.

Например, главный минор первого порядка 1 — а_ii> 0. Условия выполняются, если а_ii < 1. Главный минор второго порядка

,

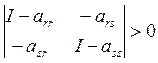Если a_rsa_sr<(1-a_rr)(1-a_ss)<1.

Матрицы, соответствующие главным минорам, также являются продуктивными. Поэтому все основные свойства матрицы A распространяются на матрицы блоков отраслей и комплексов отраслей. Главный минор n-гo порядка D, т.е. определитель матрицы (Е - А), также заключен в пределах 0 < D < 1. Отсюда, в частности, вытекает существование матрицы (Е - А)^-1.

2.  Все собственные значения матрицы .A по модулю меньше единицы.

3.  Матрица (Е — А)^-1полуположительна.

В свою очередь условие (Е - А)^-1> 0 является одним из важнейших следствий продуктивности матрицы А. Если матрица А неразложима, то матрица (Е — А)^-1 строго положительна.

Для продуктивности матрицы A достаточно, чтобы . Вытекающие отсюда следствия рассматривались выше.

Если матрица А продуктивна, но достаточное условие продуктивности не выполняется, то всегда можно подобрать такие новые измерители продукции (вектор Р), что это условие будет выполняться. Но если матрица А непродуктивна, то никакая система измерителей не исправит дефекта. 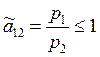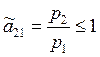Например, в рассмотренной выше производственной системе "уголь - металл" не существует таких положительных цен p_iи p₂ чтобы одновременно удовлетворялись неравенства  (или ) и  (или ).

Коэффициенты косвенных и полных народнохозяйственных затрат.. Взаимозависимости отраслей в процессе общественного производства количественно могут быть выражены системой коэффициентов прямых, косвенных и полных затрат продукции и ресурсов. Каждый коэффициент полных затрат представляет сумму прямых и косвенных затрат, обусловленных выпуском единицы определенного вида продукции. Принципиальное их отличие от коэффициентов прямых затрат состоит в том, что они являются не отраслевыми или внутрипроизводственными, а народнохозяйственными показателями.

Полные затраты на производство определенной продукции. Поставим перед собой такую задачу: определить сумму каждого вида затрат, прямо и косвенно необходимых для производства единицы продукции.

Образование полных затрат наглядно демонстрируется с помощью схемы процесса последовательного наслоения прямых и косвенных затрат, имеющей вид бесконечно ветвящегося "дерева". И образовании коэффициентов полных затрат участвуют все коэффициенты прямых затрат[2], а сам процесс бесконечен. Схема отражает особенности образования полных затрат невоспроизводимых ("внешних") ресурсов: цепочки прямых и косвенных затрат обрываются в ячейках затрат ресурсов, так как эти затраты не участвуют в процессе образования других косвенных затрат (см. ММСЭ, с. 267).

Введем дополнительные обозначения: ,  — косвенные затраты цикла mсоответственно продукции i и ресурса s; ,  - суммы прямых и косвенных затрат до цикла mвключительно соответственно продукции i и ресурса s; с_ij, F_sj — полные затраты соответственно продукции i и ресурса s.