13.4. Квазидинамические модели межотраслевого баланса продукции и производственных мощностей
При моделировании материально-вещественного аспекта процесса общественного воспроизводства в разрезе конкретных видов продукции целесообразно использовать понятие производственной мощности. Основные зависимости между капитальными вложениями, объемами производства и характеристиками воспроизводства производственных мощностей выведены в 12.2. Они являются специфическими элементами моделей межотраслевых балансов производственных мощностей, которые сочетаются с типовыми условиями, характеризующими производство и распределение продукции, использование других видов ресурсов.
Статическая модель межотраслевого баланса продукции и производственных мощностей анализировалась в 8.3.
Для перспективных предплановых расчетов применяются квазидинамические модели межотраслевого баланса продукции и производственных мощностей в детерминистской и вероятностной постановках. Квазидинамическая модель включает наряду с условиями для последнего года планового периода (балансы производства и распределения продукции, ограничения по производственным мощностям, трудовым ресурсам и т.п.) также ограничение по объему капитальных вложений, расходуемых на создание производственных мощностей за весь плановый период. Она отличается от рассматривавшихся выше моделей с обратной рекурсией тем, что не содержит в явном виде "связки" между капитальными затратами последнего года и суммой капитальных вложений за плановый период.
Рассмотрим модели, разработанные в ИЭиОПП СО АН СССР. Основная модель в детерминистской постановке по своей структуре наиболее близка к оптимизационной модели с обратной рекурсией, а по информационному обеспечению - к межотраслевым натурально-стоимостным балансам. Особенностями модели являются ограничения на объемы производства в последнем году планового периода:
X £ M0 + DM (13.24)
а также одно ограничение на объем капитальных вложений за весь плановый период:
hDM £ G, (13.25)
где DМ = (DMj-) — вектор-столбец приростов производственных мощностей за счет капитальных вложений; h— (hj) — вектор-строка коэффициентов капитальных вложений на прирост единицы мощностей; G— объем капитальных вложений за весь плановый период, обеспечивающий прирост производственных мощностей.
Кроме этих условий, модель включает балансы производства и распределения продукции (в упрощенной форме по сравнению с (13.7) и (13.11)) и ограничение по трудовым ресурсам в виде неравенства. Максимизируется конечная продукция в заданном ассортименте.
С использованием ранее введенных обозначений модель в целом имеет вид
X = AX + az + q
X£ M0 + DM
hDM £ G (13.26)
lX £ L
X³ 0; DM³ 0;
z ® max.
Для анализа свойств оптимальных решений, получаемых по данной модели, целесообразно провести ряд преобразований. Прежде всего систему уравнений балансов производства и распределения продукции и ограничения по трудовым ресурсам можно выразить относительно максимизируемой величины z:
X= bz + Q; (13.27)
pz £ (13-28)
где
![]() ,
,
Q = (Qi) = (E - A)-1 q.
![]() ;
;
![]()
Естественным
требованием является ![]() >0. Поскольку X³0 при z³ 0, то уравнения
балансов производства и распределения продукции могут быть исключены из оптимизационной
задачи путем подстановки (13.27) в (13.24). Получаем сокращенную запись модели
относительно неизвестных zи DМ:
>0. Поскольку X³0 при z³ 0, то уравнения
балансов производства и распределения продукции могут быть исключены из оптимизационной
задачи путем подстановки (13.27) в (13.24). Получаем сокращенную запись модели
относительно неизвестных zи DМ:
![]() ;
;
hDM £ G(13.29)
pz £ ![]()
DM³ 0;
z ® max.
В данной модели максимум z при сколь угодно больших капитальных вложениях ограничен сверху имеющимися трудовыми ресурсами:
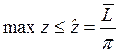 ,
,
где ![]() — трудовые ресурсы, которые остаются после
удовлетворения потребностей в фиксируемой конечной продукции; p - полные трудовые затраты на один
комплект максимизируемой конечной продукции.
— трудовые ресурсы, которые остаются после
удовлетворения потребностей в фиксируемой конечной продукции; p - полные трудовые затраты на один
комплект максимизируемой конечной продукции.
Представляет интерес взаимная по отношению к (13.29) задача определения
минимальной величины капитальных вложений для обеспечения максимального уровня
конечной продукции ![]() :
:
![]() ;
;
DM³ 0; (13.30)
hDM ®min.
Очевидно, что минимум суммы капитальных вложений достигается при
![]() , i Î I
, i Î I
Тогда
min G = C* = hDM*
Выделение капитальных вложений, превышающих величину G*, не может привести к дополнительному увеличению zиз-за дефицитности трудовых ресурсов. Заметим, что это свойство
оптимального плана обусловлено тем, что в рассматриваемой модели не отражается
связь между производительностью и фондовооруженностью труда. Решение задачи (13.29) целесообразно только при G< G*. Но тогда max ![]() , ограничение по труду выполняется как
неравенство, и поэтому его можно исключить из задачи (13.29).
, ограничение по труду выполняется как
неравенство, и поэтому его можно исключить из задачи (13.29).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.