Теоретическая механика. Часть II: Кинематика: Методические указания и контрольные задания, страница 8

Таблица 4

№ строки	Схема	см	рад	R cм	k см	t1 с
0	1			30	0,4	1
1	2			40	0,2	2
2	3			50	0,3
3	4			60	0,5	2
4				30	0,4	1
5				40	0,2	2
6				60	0,3	1
7				30	0,4
8				50	0,2	2
9				40	0,3	1
	Д	Е	Г	Б	Б	Е

                                     

                                            

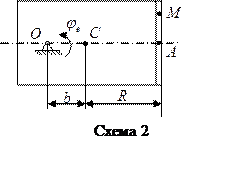
Пример выполнения задания №4

Определить абсолютную скорость и абсолютное ускорение точки М в момент времени

Дано: Схема 4

   

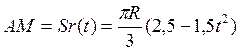
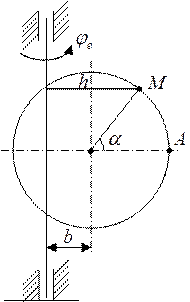
Движение точки М является сложным. Движение точки М по пластине считается относительным, движение точки М вместе с пластиной – переносное.

1)  Рассмотрим относительное движение точки М.

Положение точки М на пластине определяется расстоянием

При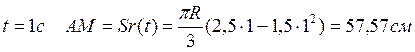

Точка движется по окружности, поэтому её положение определяется центральным углом

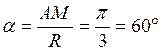
В этом положении изобразим точку М на схеме

Модуль относительной скорости

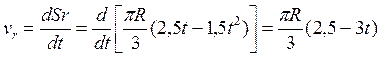
При  

Знак показывается, что вектор направлен противоположно направлению, принятому положительным.

Ускорение точки в относительном движении сказывается из нормального и тангенциального.

Нормальное ускорение

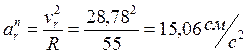
Вектор  направлен к центру окружности

Тангенциальное ускорение точки

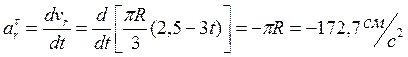
Вектор  направлен по касательной к траектории; знак показывает, что направление  противоположно положительному направлению движения точки.

2)  Рассмотрим переносное движение

Переносным является движение точки М вместе с вращающейся пластиной

Угловая скорость пластины

При

Знак показывает, что направление угловой скорости противоположно направленно угла поворота

Угловое ускорение пластины

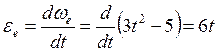
При

Направление  совпадает с направлением

Участвуя в движении пластины, точка М имеет переносную скорость, модуль которой

, где h – расстояние от точки М до оси вращения. Как видно из схемы

Вектор  направлен перпендикулярно h в сторону угловой скорости  (к нам)

В переносном движении точка М имеет ускорение

Нормальное ускорение

Вектор  направлен к оси вращения

Тангенциальное ускорение

Вектор  направлен перпендикулярно h в сторону  (от нас)

3)  Поскольку переносное движение является вращательным, следует учесть ускорение Кориолиса, модуль которого

где  - угол между направлением вектора относительной скорости  и осью переносного вращения

Для определения направления ускорения Кориолиса следует вектор относительной скорости  спроецировать на плоскость, перпендикулярную оси вращения, и повернуть эту проекцию на 90˚ в сторону . Таким образом, вектор направлен к нам.

3)  Определение абсолютной скорости

Абсолютную скорость точки М можно найти как векторную сумму относительной и переносной скорости

Учитывая, что в рассматриваемом примере угол между векторами и  составляет 90˚, применим теорему Пифагора

5)  Определение углового ускорения

Абсолютное ускорение точки М определяется как векторная сумма ускорений относительного, переносного и Кориолиса

Для определения модуля полного ускорения точки М спроецируем это векторное равенство на координатные оси.

Зная проекции абсолютного ускорения точки, модуль его определяем по теореме Пифагора

Ответ: ;