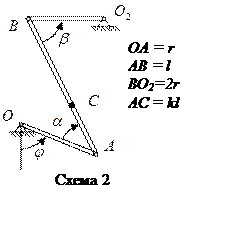Теоретическая механика. Часть II: Кинематика: Методические указания и контрольные задания, страница 6

Примечание: положительные направления  и  против ходя часовой стрелки; отрицательное – по часовой стрелке.

 

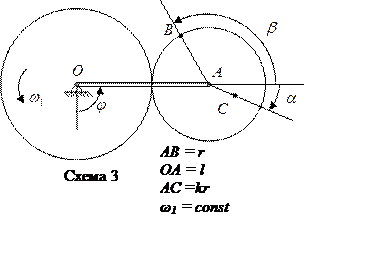
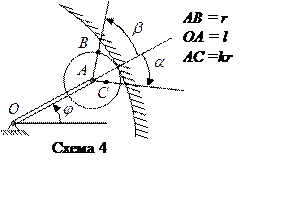
Пример 1 выполнения 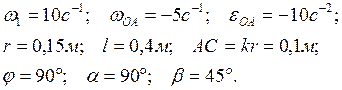задания №3

Дано:

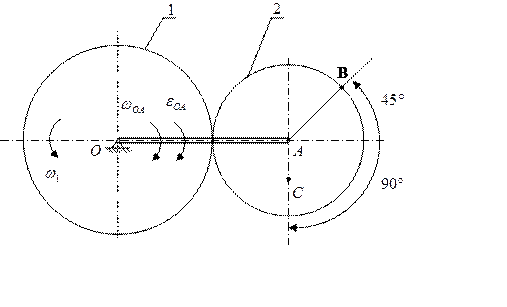
1) Определение скоростей точек

Точка А, двигаясь вместе с кривошипом ОА, который совершает вращательное движение, имеет линейную скорость

Вектор направлен перпендикулярно расстоянию ОА в ту сторону, куда указывает угловая скорость

Точка контакта колёс К, участвуя вместе с колесом 1 во вращательном движении, имеет линейную скорость

Вектор  направлен перпендикулярно ОК в ту сторону, куда указывает

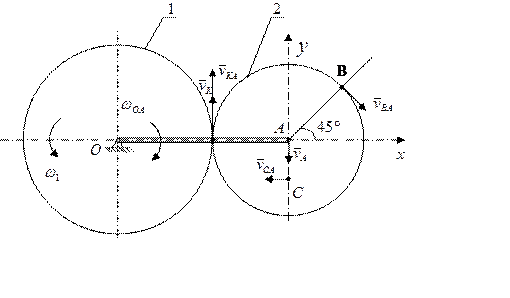
Колесо 2 совершает плоскопараллельное движение. Если принять за полюс точку А, скорость любой точки колеса можно найти как векторную сумму скорости точки А (полюса) и скорости поворота этой точки относительно точки А. Так, скорость точки К

где  - скорость поворота точки К относительно точки А, направлена перпендикулярно АК. Предположим, что  направлена вверх.

Спроецируем векторное равенство (1) на ось y:

 откуда

Величина  получилась положительной, следовательно, вектор  направлен верно.

Угловая скорость поворота колеса 2

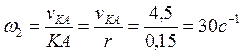
Вектор  указывает направление  (по часовой стрелке)

Скорость точки В колеса 2 можно определить, используя аналогичное равенство:

       (2)

где  - скорость поворота точки В относительно точки А

Вектор  направлен перпендикулярно ВА в ту сторону, куда указывает

Спроецируем равенство (2) на координатные оси:

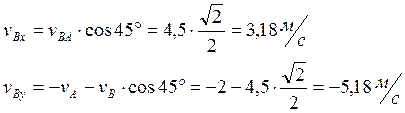
Определим величину скорости точки В по её проекциям:

Аналогичное равенство можно записать для точки С колеса 2

       (3)

где  - скорость поворота точки С относительно точки А

Вектор  направлен перпендикулярно СА в ту сторону, куда указывает

Учитывая направления векторов  и  (угол 90˚), применим теорему Пифагора:

2) Определение ускорений точек

Точка А, участвуя вместе с кривошипом ОА в его вращательном движении, имеет нормальное и тангенциальное ускорения.

Нормальное ускорение точки А

Вектор  направлен от точки А к точке О

Тангенциальное ускорение точки А

Вектор  направлен перпендикулярно ОА в ту сторону, куда указывает

   

Для определения ускорения точки В примем точку А за полюс, тогда

где  - ускорение, которое имеет точка В при повороте колеса относительно полюса. Оно в общем случае складывается из нормального и тангенциального ускорений

где  - нормальное ускорение движения точки В относительно полюса А

Вектор  направлен от точки В к полюсу А

 - тангенциальное ускорение движения точки В относительно полюса А

где  – угловое ускорение колеса 2

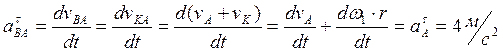
откуда угловое ускорение колеса 2 определяется

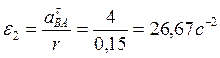, направлено так же, как

Окончательно, ускорение точки В определяется равенством

             (4)

Проецируя равенство (4) на координатные оси

найдём полное ускорение точки В

Ускорение точки С определяем аналогично

где  - ускорение движения точки С относительно точки А, складывающееся из нормального и тангенциального

Нормальное ускорение

Вектор  направлен от точки С к точке А (полюсу)

Тангенциальное ускорение

Вектор  направлен перпендикулярно СА в ту сторону, куда указывает

Окончательно

             (5)

Проецируя на координатные оси равенство (5)

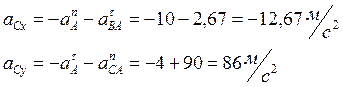
определяем ускорение точки С

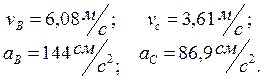Ответ:

Пример 2 выполнения задания №3

Для заданного положения механизма определить скорости и  ускорения точек В и С.

Дано:     

    

Находим:

Изображаем механизм в заданном положении

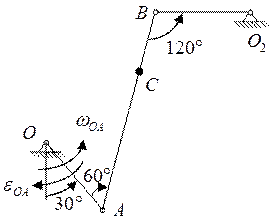
1) Определение скоростей точек

Точка А, участвуя во вращательном движении вместе с кривошипом ОА, имеет линейную скорость

Вектор  направлен перпендикулярно ОА в ту сторону, куда указывает .

Точка В принадлежит одновременно шатуну АВ и коромыслу ВО₂. Участвуя в движении коромысла ВО₂, точка В имеет скорость, направление которой перпендикулярно ВО₂ (либо вверх, либо вниз на схеме).