Теоретическая механика. Часть II: Кинематика: Методические указания и контрольные задания, страница 2

(1.1)

где

(1.2)

- координаты точки М. определяющие закон её движения в зависимости от времени t;  - нормированный базис О_xyz. М₀ – положение точки М в начальный момент времени t = t₀.

Скоростью точки М, определяющей как быстро и в каком направлении она движется в данный момент времени t, называют предел

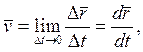
(1.3)

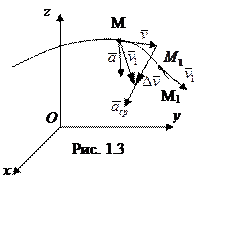 Где 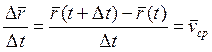 - средняя скорость точки за время  (рис. 1.2). Так как предельным положением секущей ММ₁ является касательная к траектории L точки, то и вектор её скорости  в данный момент времени t направлен по касательной к L в сторону движения. Величину 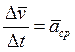 называют средним

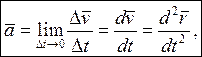
(1.4)

ускорением точки за время . Предел отношения, характеризующий изменение скорости в данный момент времени t, называют ускорением точки. Из рис. 1.3 видно, что ускорение, являющееся пределом для , направлено в сторону вогнутости траектории.

Согласно (1.1), векторы  и  можно представить в виде сумм их составляющих по осям координат

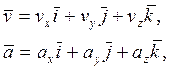
(1.5)

где

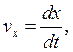
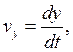
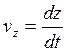
(1.6)

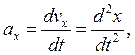
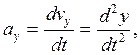
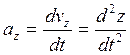
(1,7)

- проекции  и  она оси координат.

Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам

(1.8)

а направления  и  характеризуют их направляющие косинусы

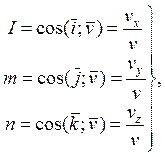
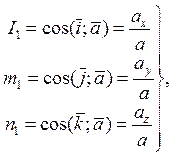
(1.9)

Таким образом, при координатном способе задания движения точки (1.2) соотношения (1.5)-(1.9) позволяют аналитически определить её скорость и ускорение.

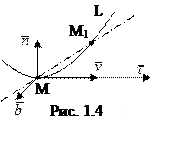
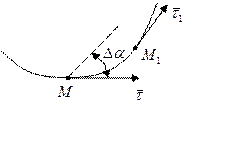Коснёмся кратко некоторых геометрических понятий, связанных с траекторией точки М как кривой L в пространстве (рис. 1.2, 1.4). Напомним, что предельное положение прямой, проходящей через точки М и М₁ кривой, когда М₁ стремится к М, определяет касательную к этой кривой в точке М. Обозначим  - единичный направляющий вектор касательной к L  в точке М. Соприкасающуюся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М₁, на ней, когда М₁ стремится к М. Нормаль  к кривой в точке М, лежащую в соприкасающейся плоскости. Называют главной нормалью к кривой в точке М. Нормаль  к кривой, перпендикулярную соприкасающейся плоскости, называют бинормалью. Прямоугольную систему взаимно ортогональных осей, направленных по ,, называют естественными осями кривой L (рис. 1.4). В механике обычно принимают направление вектора скорости за положительное направление касательной . Положительное направление главной нормали считают в строну вогнутости кривой. А бинормаль направляют так, чтобы получившаяся система осей ,, является правой.

Если  - единичный вектор касательной к кривой в точке М₁, где ММ₁ = , то угол  между   и  называют углом смежности (рис. 1.5). Кривизной «k» кривой L в точке М называют предел

(1.10)

Радиусом кривизны «ρ» кривой L в точке М называют величину обратную её кривизне в этой точке

(1.11)

Так, например, дуга окружности длиной s, опирающаяся на центральный угол α, выражается зависимостью , где R – радиус окружности. Поэтому для окружности имеем.

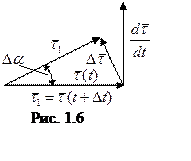Дифференцируя равенство , получим 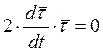, что говорит об ортогональности векторов  и . Направление вектора  является предельным для  при  и, следовательно, находясь в соприкасающейся плоскости кривой-траектории (рис. 1.6) он может быть представлен в виде

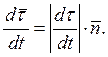
Так как с точностью до малых величин более высокого порядка , то 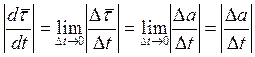 и, соответственно,