Механика \ Теоретическая механика

Теоретическая механика. Часть II: Кинематика: Методические указания и контрольные задания, страница 3


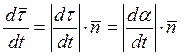
(1.12)


При естественном способе определения движения точки должны быть известны её траектория и дуговая координата как функция времени . Должно быть указано также начало отсчёта и положительное направление движения. Скорость точки, как уже было отмечено, направлена по касательной к траектории, а её величина и направление определены величиной и знаком  производной

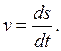(1.13)

Так как в естественных осях траектории скорость может быть представлена в виде , то. Дифференцируя это соотношение по времени, получим ускорение


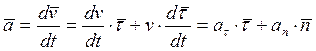
(1.14)


или


(1.15)


где


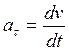
(1.16)


и согласно (1.14), (1.12), (1.11),


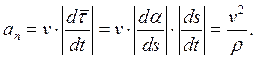
(1.17)


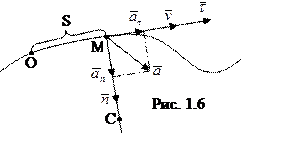Итак, ускорение точки можно разложить на тангенциальное, направленное по касательной к траектории и характеризующее изменение величины скорости, и нормальное , направленное по главной нормали к центру кривизны С траектории и определяющее изменение направления  (рис. 1.7). Очевидно, что абсолютная величина  может быть определена по формуле


(1.18)

Задание № 1

1.  Найти уравнение траектории точки и построить её.

2.  В данное время определить скорость и ускорение точки, найти касательное и нормальное ускорения, а также радиус кривизны траектории.

3.  По результатам расчётов построить векторы скорости и её ускорений в соответствующих масштабах.

Данные для своей задачи выбрать из таблицы 1 согласно шифра.

Таблица 1

№ строки

Уравнение движения

А

B

C

D

t1

(с)

 см

 см

0

-5

3

-3

0

1

1

4

2

2

1

2

2

-2

-3

-2

2

1

3

-3

-2

1

3

2

4

-4

-

-

-2

-

5

-1

-

-

-1

-

6

2

-

-

0

-

7

1

-

-

-3

-

8

3

-

-

2

-

9

5

-

-

1

-

Е

Г

Д

Д

Б

Д

Пример выполнения Задания № 1

Определить вид траектории точки; для момента времени t1=1 c найти её скорость и ускорение, нормальное и тангенциальное ускорения, радиус кривизны траектории.

Движение точки задано её координатами:

(1)

(2)
 

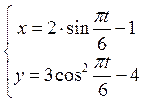
Чтобы получить уравнение траектории точки, нужно исключить время t из уравнений её движения. Для этого выразим из (1)

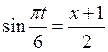
И подставим это значение во (2), учтя, что

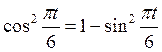
Получаем:

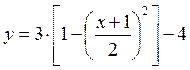 или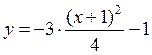

Траекторией  точки является парабола, ветви которой направлены вниз, а вершина смещена на -1 см по оси x и на -1 см по оси y (см. схему)

В момент времени t1 = 1c точка имеет координаты:

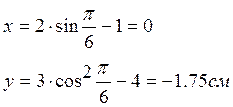
Скорость точки определяем по её проекциям на координатные оси:

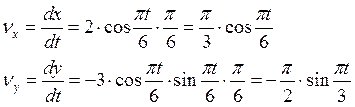
При t1 = 1 c

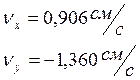
Величина скорости точки определяется по теореме Пифагора:

Аналогично скорости найдём ускорение точки:

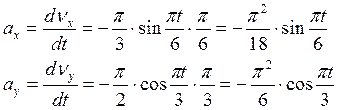
При t1 = 1 c

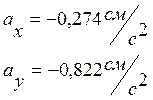
Величина полного ускорения:

Для определения тангенциального ускорения продифференцируем по времени выражение:

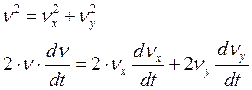
откуда

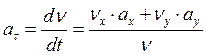
При t1 = 1 c

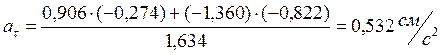
Нормальное ускорение найдём из условия, что полное ускорение определяется векторной суммой

, или с учётом направлений

; откуда

поскольку величина ,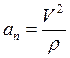

радиус кривизны .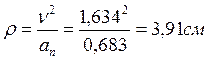

Ответ: траекторией точки является парабола;

; ; ; ;


§2. Простейшие движения тела

К простейшим относят поступательное движение тела и вращение его вокруг неподвижной оси (вращательное).

Скачать файл